Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tự vẽ hình
Ta có:
AC=OA+OCAC=OA+OC
BD=OB+ODBD=OB+OD
mà AC=BDAC=BD (gt) , OA=OBOA=OB (gt)
⇒OC=OD⇒OC=OD
Xét △OAD△OAD và △OBC△OBC có
OA=OBOA=OB (gt)
ˆAOD=ˆBOCAOD^=BOC^ (đối đỉnh)
OD=OCOD=OC (cmt)
⇒△OAD=△OBC⇒△OAD=△OBC (c.g.c)
⇒AD=BC⇒AD=BC (hai cạnh tương ứng)
b)
Do △OAD=△OBC△OAD=△OBC (cmt)
⇒ˆODA=ˆOCB⇒ODA^=OCB^ (hai góc tương ứng)
và ˆOAD=ˆOBCOAD^=OBC^ (hai góc tương ứng)
Ta có:
ˆOAD+ˆCAE=1800OAD^+CAE^=1800
ˆOBC+ˆDBE=1800OBC^+DBE^=1800
mà ˆOAD=ˆOBCOAD^=OBC^ (cmt)
⇒ˆCAE=ˆDBE⇒CAE^=DBE^
Xét △EAC△EAC và △EBD△EBD có
ˆCAE=ˆDBECAE^=DBE^ (cmt)
AC=BDAC=BD (gt)
ˆACE=ˆEDBACE^=EDB^ (do ˆOCB=ˆODAOCB^=ODA^ -cmt)
⇒△EAC=△EBD⇒△EAC=△EBD (g.c.g)
c)
Xét △AOB△AOB có OA=OBOA=OB (gt)
⇒△AOB⇒△AOB cân tại OO
⇒ˆOBA=ˆOAB⇒OBA^=OAB^
Xét △COD△COD có OC=ODOC=OD (cmt)
⇒△COD⇒△COD cân tại OO
⇒ˆOCD=ˆODC⇒OCD^=ODC^
Ta có:
ˆAOB+ˆOBA+ˆOAB=1800AOB^+OBA^+OAB^=1800
ˆCOD+ˆOCD+ˆODC=1800COD^+OCD^+ODC^=1800
mà ˆOBA=ˆOABOBA^=OAB^(cmt), ˆOCD=ˆODCOCD^=ODC^ (cmt)
⇒ˆAOB+2ˆOBA=1800⇒AOB^+2OBA^=1800
ˆCOD+2ˆODC=1800COD^+2ODC^=1800
mà ˆAOB=ˆCODAOB^=COD^ (đối đỉnh)
⇒ˆOBA=ˆODC⇒OBA^=ODC^
mà chúng ở vị trí so le trong
⇒AB//CD
a.OC=OA+AC
OD=OB+BD
mà OA=OB(gt);AC=BD(gt)
=>OC=OD
Xét tam giác OAD và tam giác OBC có:OA=OB(gt)
góc O chung
OD=OC(cmt)
=>tam giác OAD=tam giác OBC(c.g.c)=>AD=BC(hai cạnh tương ứng)(đpcm)
b.tam giác OAD=tam giác OBC(câu a)=>góc OAD=góc OBC(hai góc tương ứng)
góc ODA=góc OCB(hai góc tương ứng) hay góc BDE=góc ACE
góc OAD+góc DAC=180 độ (hai góc kề bù)
góc OBC+góc CBD=180 độ (hai góc kề bù)
=>góc DAC=góc CBD hay góc EAC=góc EBD
Xét tam giác EAC và tam giác EBD có:
Góc ACE=góc BDE(cmt)
AC=BD(gt)
góc EAC=góc EBD(cmt)
=>tam giác EAC=tam giác EBD(g.c.g)(đpcm)
c.tam giác EAC=tam giác EBD(câu b)=>EC=ED(hai cạnh tương ứng)
Xét tam giác OEC và tam giác OED có:
OC=OD(câu a)
EC=ED(cmt)
OE chung
=>tam giác OEC=tam giác OED(c.c.c)
=>góc EOC=góc EOD(hai góc tương ứng)=>OE là phân giác góc COD hay OE là phân giác góc xOy (đpcm)
a. Ta có: OD = OB + BD; OC = OA + AC.
Mà OA = OB (gt); BD = AC (gt).
=> OD = OC.
Xét tam giác AOD và tam giác BOC có:
+ OA = OB (gt).
+ \(\widehat{O}\) chung.
+ OD = OC (cmt).
=> Tam giác AOD = Tam giác BOC (c - g - c).
=> AD = BC (Cặp cạnh tương ứng).
b. Tam giác AOD = Tam giác BOC (c - g - c).
=> \(\widehat{OAD}=\widehat{OBC}\) (2 góc tương ứng).
Mà \(\widehat{OAD}+\widehat{DAC}=180^o;\widehat{OBC}+\widehat{CBD}=180^o.\)
=> \(\widehat{DAC}=\widehat{CBD}.\)
hay \(\widehat{EAC}=\widehat{EBD}.\)
c) Tam giác AOD = Tam giác BOC (cmt).
=> \(\widehat{ODA}=\widehat{OCB}\) (2 góc tương ứng).
Xét tam giác EBD và tam giác EAC:
+ \(\widehat{BDE}=\widehat{ACE}\left(\text{}\widehat{ODA}=\widehat{OCB}\right).\) (cmt).
+ BD = AC (gt).
+ \(\widehat{EBD}=\widehat{EAC}\left(cmt\right).\)
=> Tam giác EBD = Tam giác EAC (g - c - g).
=> BE = AE (2 cạnh tương ứng).
Xét tam giác OBE và tam giác OAE:
+ OB = OA (gt).
+ OE chung.
+ BE = AE (cmt).
=> Tam giác OBE = Tam giác OAE (c - c - c).
=> \(\widehat{BOE}=\widehat{AOE}\) (2 góc tương ứng).
=> OE là phân giác của \(\widehat{xOy}\left(đpcm\right).\)
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{AOD}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Xét ΔBDC và ΔACD có
BD=AC
\(\widehat{BDC}=\widehat{ACD}\)
DC chung
Do đó: ΔBDC=ΔACD
Suy ra: \(\widehat{EAC}=\widehat{EBD}\)
Xét ΔEAC và ΔEBD có
\(\widehat{EAC}=\widehat{EBD}\)
AC=BD
\(\widehat{ECA}=\widehat{EDB}\)
Do đó: ΔEAC=ΔEBD
c: Xét ΔOEC và ΔOED có
OE chung
EC=ED
OC=OD
Do đó: ΔOEC=ΔOED
Suy ra: \(\widehat{COE}=\widehat{DOE}\)
hay OE là tia phân giác của góc xOy
EAC = 
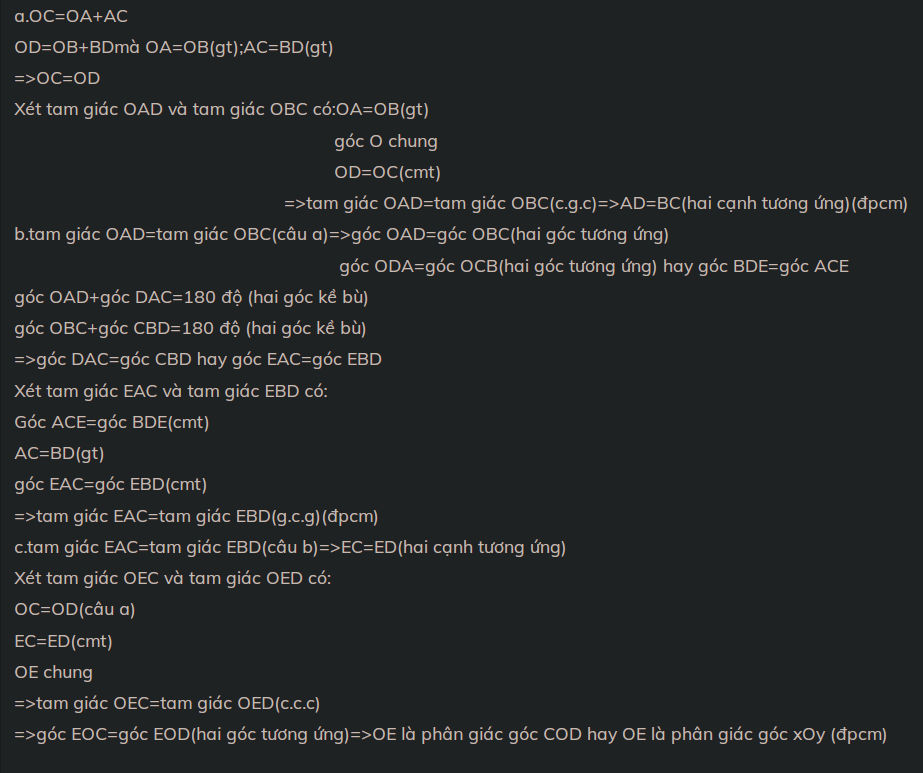
a) Ta có:
\(\left\{{}\begin{matrix}OA+AC=OC\\OB+BD=OD\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}OA=OB\left(gt\right)\\AC=BD\left(gt\right)\end{matrix}\right.\)
=> \(OC=OD.\)
Xét 2 \(\Delta\) \(OBC\) và \(OAD\) có:
\(OB=OA\left(gt\right)\)
\(\widehat{O}\) chung
\(OC=OD\left(cmt\right)\)
=> \(\Delta OBC=\Delta OAD\left(c-g-c\right)\)
=> \(BC=AD\) (2 cạnh tương ứng).
b) Theo câu a) ta có \(\Delta OBC=\Delta OAD.\)
=> \(\left\{{}\begin{matrix}\widehat{OCB}=\widehat{ODA}\\\widehat{OBC}=\widehat{OAD}\end{matrix}\right.\) (các góc tương ứng).
\(\widehat{OCB}=\widehat{ODA}\Rightarrow\widehat{ECA}=\widehat{EDB}.\)
Ta có:
\(\left\{{}\begin{matrix}\widehat{OAD}+\widehat{DAC}=180^0\\\widehat{OBC}+\widehat{CBD}=180^0\end{matrix}\right.\) (các góc kề bù).
Mà \(\widehat{OAD}=\widehat{OBC}\left(cmt\right)\)
=> \(\widehat{DAC}=\widehat{CBD}.\)
Hay \(\widehat{EAC}=\widehat{EBD}.\)
Xét 2 \(\Delta\) \(EAC\) và \(EBD\) có:
\(\widehat{EAC}=\widehat{EBD}\left(cmt\right)\)
\(AC=BD\left(gt\right)\)
\(\widehat{ECA}=\widehat{EDB}\left(cmt\right)\)
=> \(\Delta EAC=\Delta EBD\left(g-c-g\right).\)
c) Vì \(\widehat{OCB}=\widehat{ODA}\left(cmt\right)\)
=> \(\widehat{OCE}=\widehat{ODE}.\)
Xét 2 \(\Delta\) \(OEC\) và \(OED\) có:
\(OC=OD\left(cmt\right)\)
\(\widehat{OCE}=\widehat{ODE}\left(cmt\right)\)
Cạnh OE chung
=> \(\Delta OEC=\Delta OED\left(c-g-c\right)\)
=> \(\widehat{COE}=\widehat{DOE}\) (2 góc tương ứng).
=> \(OE\) là tia phân giác của \(\widehat{COD}.\)
Hay \(OE\) là tia phân giác của \(\widehat{xOy}\left(đpcm\right).\)
Chúc bạn học tốt!
ko có giả thiết, kết luận hả bạn