\(\dfrac{x}{3}=\dfrac{y}{7}\) ; \(\dfrac{y}{2}=\dfrac{z}{5}\) và \(x+y+z=-10\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 9 2021
a) Ta có: \(\dfrac{x}{y}=\dfrac{10}{9}\Rightarrow\dfrac{x}{10}=\dfrac{y}{9}\)
\(\dfrac{y}{z}=\dfrac{3}{4}\Rightarrow\dfrac{y}{3}=\dfrac{z}{4}\Rightarrow\dfrac{y}{9}=\dfrac{z}{12}\)
\(\Rightarrow\dfrac{x}{10}=\dfrac{y}{9}=\dfrac{z}{12}=\dfrac{x-y+z}{10-9+12}=\dfrac{78}{13}=6\)
\(\Rightarrow\left\{{}\begin{matrix}x=6.10=60\\y=6.9=54\\z=6.12=72\end{matrix}\right.\)
b)Ta có: \(\dfrac{x}{y}=\dfrac{9}{7}\Rightarrow\dfrac{x}{9}=\dfrac{y}{7}\)
\(\dfrac{y}{z}=\dfrac{7}{3}\Rightarrow\dfrac{y}{7}=\dfrac{z}{3}\)
\(\Rightarrow\dfrac{x}{9}=\dfrac{y}{7}=\dfrac{z}{3}=\dfrac{x-y+z}{9-7+3}=-\dfrac{15}{5}=-3\)
\(\Rightarrow\left\{{}\begin{matrix}x=-3.9=-27\\y=-3.7=-21\\z=-3.3=-9\end{matrix}\right.\)
c) \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{3}\)
\(\Rightarrow\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{z^2}{9}=\dfrac{x^2+y^2+z^2}{9+16+9}=\dfrac{200}{34}=\dfrac{100}{17}\)
\(\Rightarrow\left\{{}\begin{matrix}x^2=\dfrac{900}{17}\\y^2=\dfrac{1600}{17}\\z^2=\dfrac{900}{17}\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=\pm\dfrac{30\sqrt{17}}{17}\\y=\pm\dfrac{40\sqrt{17}}{17}\\z=\pm\dfrac{30\sqrt{17}}{17}\end{matrix}\right.\)
Vậy\(\left(x;y;z\right)\in\left\{\left(\dfrac{30\sqrt{17}}{17};\dfrac{40\sqrt{17}}{17};\dfrac{30\sqrt{17}}{17}\right),\left(-\dfrac{30\sqrt{17}}{17};-\dfrac{40\sqrt{17}}{17};-\dfrac{30\sqrt{17}}{17}\right)\right\}\)
20 tháng 8 2021
1) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{5}=\dfrac{y}{7}=\dfrac{x+y}{5+7}=\dfrac{48}{12}=4\)
\(\dfrac{x}{5}=4\Rightarrow x=20\\ \dfrac{y}{7}=4\Rightarrow y=28\)
2) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{4}=\dfrac{y}{-7}=\dfrac{x-y}{4+7}=\dfrac{33}{11}=3\)
\(\dfrac{x}{4}=3\Rightarrow x=12\\ \dfrac{y}{-7}=3\Rightarrow y=-21\)
9 tháng 5 2022
a) \(\dfrac{x}{y}\times\dfrac{3}{4}=\dfrac{5}{6}+\dfrac{1}{3}\)
\(\dfrac{x}{y}\times\dfrac{3}{4}=\dfrac{7}{6}\)
\(\dfrac{x}{y}=\dfrac{7}{6}:\dfrac{3}{4}\)
\(\dfrac{x}{y}=\dfrac{14}{9}\)
b) \(\dfrac{7}{9}:\dfrac{x}{y}=\dfrac{10}{7}-\dfrac{13}{14}\)
\(\dfrac{7}{9}:\dfrac{x}{y}=\dfrac{1}{2}\)
\(\dfrac{x}{y}=\dfrac{7}{9}:\dfrac{1}{2}\)
\(\dfrac{x}{y}=\dfrac{14}{9}\)
MH
9 tháng 5 2022
Bài 1:
+) \(\dfrac{7}{8}\times y=\dfrac{3}{2}+\dfrac{6}{4}=3\)
\(y=3:\dfrac{7}{8}=\dfrac{24}{7}\)
+) \(\dfrac{1}{y}\times\left(\dfrac{2}{5}+\dfrac{1}{5}\right)=\dfrac{10}{3}\)
\(\dfrac{1}{y}=\dfrac{10}{3}:\dfrac{3}{5}=\dfrac{50}{9}\)
\(y=\dfrac{9}{50}\)
HP
31 tháng 10 2021
1. Ta có: \(\dfrac{x}{-7}=\dfrac{y}{4}\Rightarrow\dfrac{2x}{-14}=\dfrac{3y}{12}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x-3y}{-14-12}=\dfrac{-78}{-26}=3\)
=> \(\left\{{}\begin{matrix}x=-21\\y=12\end{matrix}\right.\)
2. Ta có:
- \(\dfrac{x}{y}=\dfrac{9}{7}\Rightarrow\dfrac{x}{9}=\dfrac{y}{7}\)
- \(\dfrac{y}{z}=\dfrac{7}{3}\Rightarrow\dfrac{y}{7}=\dfrac{z}{3}\)
=> \(\dfrac{x}{9}=\dfrac{y}{7}=\dfrac{z}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{x-y+z}{9-7+3}=\dfrac{-15}{5}=-3\)
=> \(\left\{{}\begin{matrix}x=-27\\y=-21\\z=-9\end{matrix}\right.\)
10 tháng 7 2022
\(\dfrac{x}{y}=\dfrac{3}{7}.\\ \Rightarrow x=\dfrac{3}{7}y.\\ x-y=16.\\\Rightarrow\dfrac{3}{7}y-y=16.\\ \Rightarrow y=-28.\\ \Rightarrow x=-12.\)
\(\dfrac{x}{1,8}=\dfrac{y}{3,2}.\\ \Rightarrow\dfrac{x}{y}=\dfrac{1,8}{3,2}=\dfrac{9}{16}.\\ \Rightarrow x=\dfrac{9}{16}y.\\ y-x=7.\\ \Rightarrow y-\dfrac{9}{16}y=7.\\ \Leftrightarrow y=16.\\ \Leftrightarrow x=9.\)
\(\dfrac{x}{5}=\dfrac{y}{8}.\\ \Rightarrow\dfrac{x}{y}=\dfrac{5}{8}.\\ \Rightarrow x=\dfrac{5}{8}y.\\ x+2y=42.\\ \Rightarrow\dfrac{5}{8}y+2y=42.\\ \Leftrightarrow y=16.\\ \Rightarrow x=10.\)
\(\dfrac{x}{5}=\dfrac{y}{7}.\\ \Rightarrow\dfrac{x}{y}=\dfrac{5}{7}.\\ \Rightarrow x=\dfrac{5}{7}y.\\ x.y=35.\\ \Rightarrow\dfrac{5}{7}y.y=35.\\ \Leftrightarrow y^2=49.\\ \Leftrightarrow u=\pm7.\\ \Rightarrow x=\pm5.\)
6 tháng 11 2021
1: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{11}=\dfrac{y-x}{11-8}=\dfrac{-42}{3}=-14\)
Do đó: x=-112;y=-154
MH
5 tháng 10 2021
a) \(\dfrac{x}{y}=\dfrac{9}{7}\)⇒\(\dfrac{x}{9}=\dfrac{y}{7}\)
\(\dfrac{y}{z}=\dfrac{7}{3}\)⇒\(\dfrac{y}{7}=\dfrac{z}{3}\)
⇒\(\dfrac{x}{9}=\dfrac{y}{7}=\dfrac{z}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau,ta có:
\(\dfrac{x}{9}=\dfrac{y}{7}=\dfrac{z}{3}=\dfrac{x-y+z}{9-7+3}=-\dfrac{15}{5}=-3\)
⇒\(\left\{{}\begin{matrix}x=-3.9=-27\\y=-3.7=-21\\z=-3.3=-9\end{matrix}\right.\)
5 tháng 10 2021
c: Ta có: 5x=8y=20z
nên \(\dfrac{x}{\dfrac{1}{5}}=\dfrac{y}{\dfrac{1}{8}}=\dfrac{z}{\dfrac{1}{20}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{5}}=\dfrac{y}{\dfrac{1}{8}}=\dfrac{z}{\dfrac{1}{20}}=\dfrac{x-y-z}{\dfrac{1}{5}-\dfrac{1}{8}-\dfrac{1}{20}}=\dfrac{3}{\dfrac{1}{40}}=120\)
Do đó: x=24; y=15; z=6
TG
14 tháng 1 2021
a) ĐKXD: x ≠ 2
\(\dfrac{1}{x-2}+3=\dfrac{3-x}{x-2}\)
\(\Leftrightarrow\dfrac{1}{x-2}-\dfrac{3-x}{x-2}=-3\)
\(\Leftrightarrow\dfrac{1-3+x}{x-2}=-3\)
\(\Leftrightarrow\dfrac{-2+x}{x-2}=-3\)
\(\Leftrightarrow-2+x=-3\left(x-2\right)\)
\(\Leftrightarrow-2+x=-3x+6\)
\(\Leftrightarrow x+3x=6+2\)
\(\Leftrightarrow4x=8\)
\(\Leftrightarrow x=2\) (loại vì không thỏa mãn điều kiện)
Vậy S = ∅
b) ĐKXĐ: x ≠ 7
\(\dfrac{8-x}{x-7}-8=\dfrac{1}{x-7}\)
\(\Leftrightarrow\dfrac{8-x}{x-7}-\dfrac{1}{x-7}=8\)
\(\Leftrightarrow\dfrac{7-x}{x-7}=8\)
\(\Leftrightarrow-1=8\left(vô-lý\right)\)
Vậy S = ∅
P/s: Ko chắc ạ!
TG
14 tháng 1 2021
c) ĐKXĐ: x ≠ 1
\(\dfrac{1}{x-1}+\dfrac{2x}{x^2+x+1}=\dfrac{3x^2}{x^3-1}\)
Quy đồng và khử mẫu ta được:
\(x^2+x+1+2x\left(x-1\right)=3x^2\)
\(\Leftrightarrow x^2+x+1+2x^2-2x-3x^2=0\)
\(\Leftrightarrow-x+1=0\)
\(\Leftrightarrow x=1\) (loại vì ko t/m đk)
Vậy S = ∅
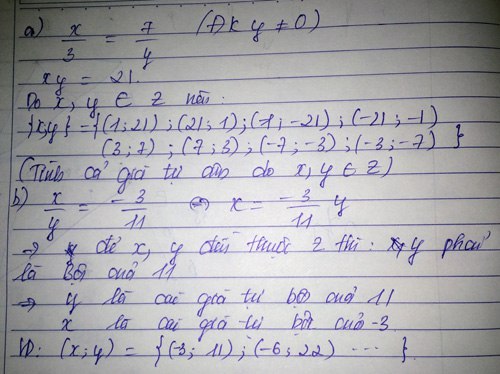
GIÚP MÌNH VỚI MN ƠIIIII!
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{6}=\dfrac{y}{14}=\dfrac{z}{35}=\dfrac{x+y+z}{6+14+35}=\dfrac{-10}{55}=\dfrac{-2}{11}\)
Do đó: \(\left\{{}\begin{matrix}x=\dfrac{-12}{11}\\y=\dfrac{-28}{11}\\z=\dfrac{-70}{11}\end{matrix}\right.\)