cho hai hàm số y = f[x] = x+1 và y = g[x] = x+\(\sqrt{\frac{4}{25}}\) . Tìm giá trị của hàm số y= f[x] để f[x] = g[0]
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
5 tháng 10 2017
Chọn C
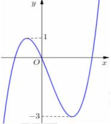
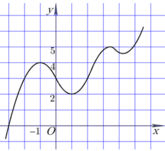
Quan sát đồ thị ta thấy hàm số y = f(x) đạt giá trị nhỏ nhất trên [-1;3] là -1 tại điểm x = =-1 và đạt giá trị lớn nhất trên[-1;3] là 4 tại điểm x = 3. Do đó M = 4, m = -1.
Giá trị M - m = 4 - (-1) = 5.
HN
0


CM
5 tháng 7 2018
Đáp án A
Ta có
![]()
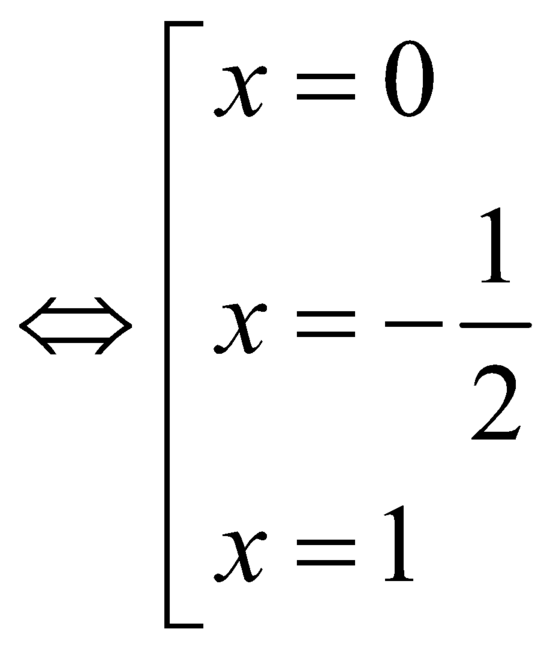 .
.
Bảng xét dấu:
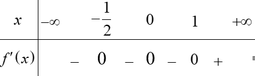
Suy ra hàm số có một điểm cực trị.

CM
10 tháng 2 2019
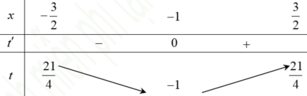
Chọn D
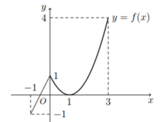
Dựa vào hình vẽ ta có : M = 3, m = -2. Do đó: M + m = 1

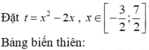




\(y=g\left(x\right)=x+\sqrt{\frac{4}{25}}\)
\(g\left(0\right)=0+\sqrt{\frac{4}{25}}=\frac{2}{5}\)
Để \(f\left(x\right)=g\left(0\right)\) thì
\(f\left(x\right)=x+1=\frac{2}{5}\)
Vậy để f(x) = g(0) thì y = f(x) = \(\frac{2}{5}\)