Cho tam giác ABC nhọn, nội tiếp (O). Đường cao BD,CƯ cắt nhau tại H. Vẽ đường kính AM của (O). CM a) BHCM là hình bình hành b) Gọi I là giao điểm của HM và BC.CM OI vuông góc BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 11 2022
a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
nên BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔDAH có DI/DH=DO/DA
nen Io//AH và IO=AH/2
=>AH=2OI
AT
25 tháng 6 2021
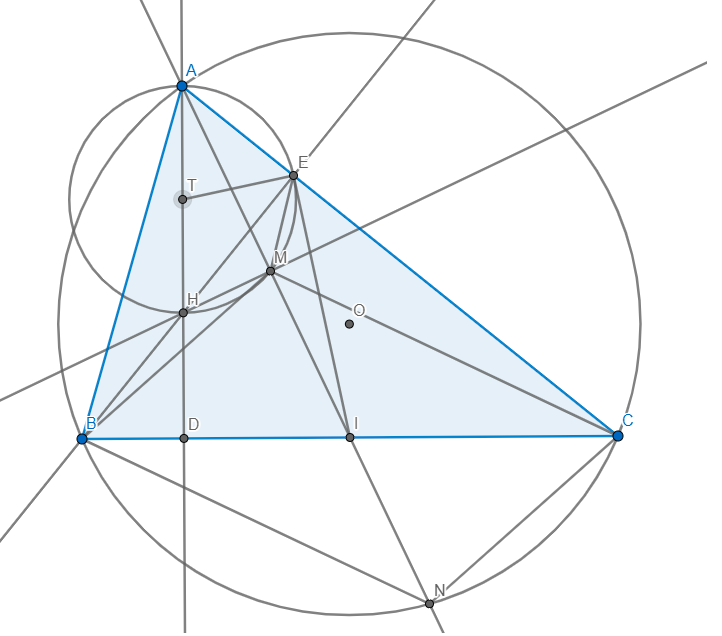
a) Ta có: \(\angle AMH=\angle AEH=90\Rightarrow AEMH\) nội tiếp
\(\Rightarrow\angle AME=\angle AHE\)
Ta có: \(\angle HEC+\angle HDC=90+90=180\Rightarrow HECD\) nội tiếp
\(\Rightarrow\angle AHE=\angle ACD\Rightarrow\angle AME=\angle ACD\Rightarrow MECI\) nội tiếp
\(\Rightarrow\angle AME=\angle ACI\)
Xét \(\Delta AME\) và \(\Delta ACI:\) Ta có: \(\left\{{}\begin{matrix}\angle AME=\angle ACI\\\angle CAIchung\end{matrix}\right.\)
\(\Rightarrow\Delta AME\sim\Delta ACI\left(g-g\right)\Rightarrow\dfrac{AM}{AC}=\dfrac{AE}{AI}\Rightarrow AE.AC=AM.AI\)
b) Gọi T là trung điểm AH
Dễ dàng chứng minh được T là tâm (AEMH)
\(\Rightarrow\Delta TEH\) cân tại T \(\Rightarrow\angle TEH=\angle THE=\angle ACB\) (HECD nội tiếp)
\(\Delta EBC\) vuông tại E có I là trung điểm BC cân tại I
\(\Rightarrow\Delta EBI\) cân tại I \(\Rightarrow\angle BEI=\angle EBI\)
mà \(\angle EBI+\angle ACB=90\Rightarrow\angle BEI+\angle TEH=90\Rightarrow\angle TEI=90\)
\(\Rightarrow IE\) là tiếp tuyến của (AEMH)
\(\Rightarrow\angle IAE=\angle IEM=\angle ICM\) (EMIC nội tiếp)
mà \(\angle IAE=\angle NBC\) (NBAC nội tiếp) \(\Rightarrow\angle ICM=\angle NBC\)
\(\Rightarrow CM\parallel BN\)
Tương tự \(\Rightarrow BM\parallel CN\) \(\Rightarrow BMCN\) là hình bình hành
mà I là trung điểm BC \(\Rightarrow I\) là trung điểm MN
8 tháng 3 2023
a, Gọi I là trung điểm của BC
Tam giác BEC vuông tại E trung tuyến EI nên IE = IB = IC
Tam giác BFC vuông tại F trung tuyến FI nên IF = IB = IC
Vậy tứ giác BEFC cùng thuộc đường tròn tâm I bán kính IB
b, Ta có :
\(\widehat{ACK}=90^0\) ( góc nội tiếp chắn nửa đường tròn )
= > BH // CK ( cùng vuông góc với AC )
Tương tự ta cũng có CH // BK
= > BHCK là hình bình hành
= > 2 đường chéo cắt nhau tại trung điểm của mỗi đường
Mà I là trung điểm của BC
= > H,I,K thẳng hàng ( đpcm )
c, Dễ thấy các tứ giác AFHE và BFHD nội tiếp nên :
\(\widehat{DFE}=\widehat{DFH}+\widehat{HFE}=\widehat{HBD}+\widehat{HAF}=2\widehat{HBD}=2.\left(90^0-\widehat{C}\right)=180^0-2\widehat{C}\)
( Do góc HBD và HAF cùng phụ với góc C )
Lại có :
Tam giác EIC cân tại I nên :
\(\widehat{EIC}=180^0-\widehat{IEC}-\widehat{ECI}=180^0-2\widehat{C}\)
\(=>\widehat{EIC}=\widehat{DFE}\)
= > Tứ giác DFEI là tứ giác nội tiếp
= > D,F,E,I cùng thuộc 1 đường tròn