Gọi x1 x2 là nghiệm của phương trình 4x2-7x-1=0 .Tìm giá trị của biểu thức M=x12+x22
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 8 2017
Ta gọi hai nghiệm của phương trình đã cho là x 1 , x 2 . Theo hệ thức Vi-et ta có: x 1 x 2 = − 2 5 x 1 + x 2 = 9 5
⇔ M = x 1 2 + x 2 2 = ( x 1 + x 2 ) 2 − 2 x 1 x 2 = 81 25 − 2 − 2 5 = 101 25
Đáp án cần chọn là: C
CM
19 tháng 11 2017
Đáp án B
Phương trình x 2 - 5 x + 2 = 0 có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có:
CM
29 tháng 9 2017
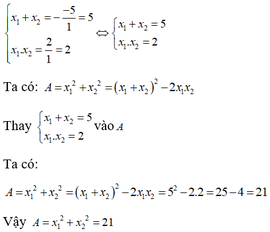
Phương trình x 2 − 5x + 2 = 0 có = ( − 5 ) 2 – 4.1.2 = 17 > 0 nên phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = − b a x 1 . x 2 = c a ⇔ x 1 + x 2 = 5 x 1 . x 2 = 2
Ta có
A = x 1 2 + x 2 2 = ( x 1 + x 2 ) 2 – 2 x 1 . x 2 = 5 2 – 2 . 2 = 21
Đáp án: B
CM
21 tháng 12 2018
Đáp án B
Phương trình x 2 - 5 x + 2 = 0 có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có:
CM
8 tháng 7 2017
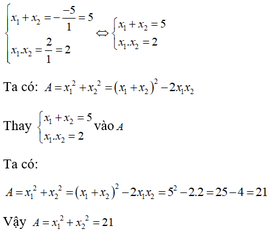
Phương trình 2 x 2 − 11x + 3 = 0 3 = 97 > 0 nên phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = − b a x 1 . x 2 = c a ⇔ x 1 + x 2 = 11 2 x 1 . x 2 = 3 2
Ta có
A = x 1 2 + x 2 2 = x 1 + x 2 2 - 2 x 1 x 2 1 + x 2 ) = 11 2 2 − 2. 3 2 = 109 4
Đáp án: A
21 tháng 1 2023
a: Δ=(2m-1)^2-4*(-m)
=4m^2-4m+1+4m=4m^2+1>0
=>Phương trình luôn có nghiệm
b: \(A=\left(x_1+x_2\right)^2-2x_1x_2-x_1x_2\)
\(=\left(2m-1\right)^2-3\left(-m\right)\)
=4m^2-4m+1+3m
=4m^2-m+1
=4(m^2-1/4m+1/4)
=4(m^2-2*m*1/8+1/64+15/64)
=4(m-1/8)^2+15/16>=15/16
Dấu = xảy ra khi m=1/8
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 4 2021
\(\Delta=a^2+8>0\Rightarrow\) pt luôn có 2 nghiệm
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=a\\x_1x_2=-2\end{matrix}\right.\)
\(N=x_1^2+x_2^2+x_1x_2+2\left(x_1+x_2\right)+4\)
\(=\left(x_1+x_2\right)^2-x_1x_2+2\left(x_1+x_2\right)+4\)
\(=a^2+2+2a+4\)
\(N=a^2+2a+6=\left(a+1\right)^2+5\ge5\)
\(N_{min}=5\) khi \(a=-1\)
7 tháng 6 2021
\(\Delta=4m^2+69\ge0\Leftrightarrow\begin{matrix}m\ge\dfrac{\sqrt{69}}{2}\\m\le-\dfrac{\sqrt{69}}{2}\end{matrix}\)
viet : \(\left\{{}\begin{matrix}x_1+x_2=7\\x_1x_2=-\left(m^2+5\right)\end{matrix}\right.\)
ta có : \(A=\left(x_1+x_2\right)^2-x_1x_2+2m=49+m^2+5+2m=m^2+2m+54\)
vì \(m\ge\dfrac{\sqrt{69}}{2}\Rightarrow m^2+2m+54\ge\dfrac{69+2\sqrt{69}+216}{4}\) hay \(A\ge\dfrac{69+2\sqrt{69}+216}{4}\)
CM
8 tháng 6 2019
Đáp án D
Đặt 3 x 2 − x = t > 0 ta được
t 2 + 3 t − 4 = 0 ⇔ t = 1 t = − 4 l o a i ⇒ 3 x 2 − x = 1 ⇔ x 2 − x = 0 ⇔ x 1 = 0 x 2 = 1
P = x 1 2 − x 2 2 = − 1 .
△= \(7^2+4.4.1=65\)
\(\Rightarrow x_1=\frac{7+\sqrt{65}}{8},x_2=\frac{7-\sqrt{65}}{8}\)
M = \(x_1^2+x_2^2=\left(\frac{7+\sqrt{65}}{8}\right)^2+\left(\frac{7-\sqrt{65}}{8}\right)^2=\frac{114+14\sqrt{65}+114-14\sqrt{65}}{64}=\frac{228}{64}=\frac{57}{16}\)
\(\Delta=49-4.\left(-1\right).4=65>0\) => pt có 2 n0 pb
\(Vi-et\Rightarrow\left\{{}\begin{matrix}x_1+x_2=\frac{7}{4}\\x_1x_2=-\frac{1}{4}\end{matrix}\right.\)
\(\Rightarrow M=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(\frac{7}{4}\right)^2-2.\left(-\frac{1}{4}\right)=\frac{57}{16}\)