Cho hình bình hành ABCD cạnh CD cố định.Biết AC=2cm tìm quỹ tích đỉnh B.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 4 2016
- Theo tính chất hình bình hành : BA=DC \(\Rightarrow\overrightarrow{AB}=\overrightarrow{CD}\). Nhưng theo giả thiết A,B cố định , cho nên \(\overrightarrow{AB}\) cố định . Ví C chạy trên (O;R) , D là ảnh của C qua phép tịnh tiến theo \(\overrightarrow{AB}\) , cho nên D chạy trên đường tròn O’ là ảnh của đường tròn O
- Cách xác định (O’) : Từ O kẻ đường thẳng // với AB , sau đó dựng véc tơ \(\overrightarrow{OO'}=\overrightarrow{AB}\). Từ O’ quay đường tròn bán kính R , đó chính là đường tròn quỹ tích của D.
21 tháng 5 2018
Sử dụng phép tịnh tiến nha
Mà tìm quỹ tích C trong trường hợp nào hã bạn ???????????
CM
30 tháng 11 2019
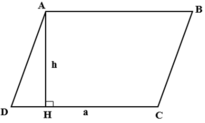
Ta có : S = a.h
Khi đó ta có: S = 4.2 = 8 c m 2 .
Chọn đáp án B.
a) Phần thuận
Gọi O là điểm đối xứng với D qua C thì O là một điểm cố định
Tứ giác ABOC có AB // OC; AB = OC (vì cùng bằng CD) nên ABOC là hình bình hành
⟹ OB = AC = 2cm. Điểm B cách điểm O cố định một khoảng 2cm nên điểm B nằm trên đường tròn tâm O bán kính 2cm.
Giới hạn: Vì B, C, D không thẳng hàng nên B nằm trên đường tròn tâm O bán kính 2cm trừ giao điểm của đường tròn này với đường thẳng CD.
b) Phần đảo
Lấy điểm B bất kì trên đường tròn tâm O bán kính 2cm (trừ giao điểm của đường tròn này với đường thẳng CD). Suy ra OB = 2cm. Vẽ hình bình hành ABCD. Ta chứng minh hình bình hành có AC = 2cm
Thật vậy, AB // CD và AB = CD ⟹ AB // CO và AB = CO. Do đó tứ giác ABOC là hình bình hành, suy ra AC = OB = 2cm
c) Kết luận
Vậy quỹ tích của điểm B là đường tròn tâm O bán kính 2cm, trừ giao điểm của đường tròn này với đường thẳng CD.