0 x 0 =
1 x 0 =
?????????????????????????
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


đăng ít thôi bạn! Nếu bạn đăng lẻ ra thì bn sẽ nhận đc sự trợ giúp nhanh hơn !

a) Ta có: \(\left|x-3\right|+\left|y-2x\right|=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\y-2x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2x=2\cdot3=6\end{matrix}\right.\)

a) Ta có: \(x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x-1=0\)hay x=1
Vậy: S={1}
c) Ta có: \(x+x^4=0\)
\(\Leftrightarrow x\left(x^3+1\right)=0\)
\(\Leftrightarrow x\left(x+1\right)\left(x^2-x+1\right)=0\)
mà \(x^2-x+1>0\forall x\)
nên x(x+1)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
Vậy: S={0;-1}

1)x^2-2x-1=0
<=> (x^2-2x+1)-2=0
<=>(x-1)2 =2
=>x-1 = \(\pm\sqrt{2}\)
=> x= \(\pm\sqrt{2}\) +1
2) x^2-x-1=0
<=> (x^2-x+1/4) -5/4=0
<=>(x+1/2)2= 5/4
=> x+1/2 = \(\pm\sqrt{\dfrac{5}{4}}\)
=>x=\(\pm\sqrt{\dfrac{5}{4}}\) - 1/2
3)x^2+x-3=0
<=> (x^2 + x + 1/4) -13/4=0
<=>(x+1/2)2 = 13/4
=> x+1/2 = \(\sqrt{\dfrac{13}{4}}\)
=> x= \(\sqrt{\dfrac{13}{4}}\) -1/2
4) 4x^2-4x-1=0
<=> (4x^2-4x+1)-2=0
<=>(2x-1)2 -2=0
<=> (2x-1)2 - \(\left(\sqrt{2}\right)^2\) =0
<=> (2x-1 - \(\sqrt{2}\) ) . (2x-1 +\(\sqrt{2}\) )=0
=> 2x-1-\(\sqrt{2}\) =0 hoặc 2x-1+\(\sqrt{2}\) =0
=> 2x= 1+\(\sqrt{2}\) hoặc 2x= 1 - \(\sqrt{2}\)
=> x=\(\dfrac{1+\sqrt{2}}{2}\) hoặc x=\(\dfrac{1-\sqrt{2}}{2}\)

a) \(2{x^2} + 3x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 2{x^2} + 3x + 1\) có 2 nghiệm phân biệt \(x = - 1,x = \frac{{ - 1}}{2}\)
hệ số \(a = 2 > 0\)
Ta có bảng xét dấu f(x) như sau:
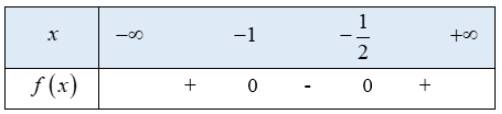
Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le - 1\\x \ge - \frac{1}{2}\end{array} \right.\)
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right] \cup \left[ { - \frac{1}{2}; + \infty } \right)\)
b) \( - 3{x^2} + x + 1 > 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + x + 1\) có 2 nghiệm phân biệt \(x = \frac{{1 - \sqrt {13} }}{6},x = \frac{{1 + \sqrt {13} }}{6}\)
Hệ số \(a = - 3 < 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) > 0\)\( \Leftrightarrow \frac{{1 - \sqrt {13} }}{6} < x < \frac{{1 + \sqrt {13} }}{6}\)
Vậy tập nghiệm của bất phương trình là \(\left( {\frac{{1 - \sqrt {13} }}{6};\frac{{1 + \sqrt {13} }}{6}} \right)\)
c) \(4{x^2} + 4x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 4{x^2} + 4x + 1\) có nghiệm duy nhất \(x = \frac{{ - 1}}{2}\)
hệ số \(a = 4 > 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow x \in \mathbb{R}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\)
d) \( - 16{x^2} + 8x - 1 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 16{x^2} + 8x - 1\) có nghiệm duy nhất \(x = \frac{1}{4}\)
hệ số \(a = - 16 < 0\)
Ta có bảng xét dấu f(x) như sau:
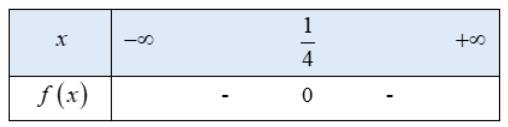
Từ bảng xét dấu ta thấy \(f\left( x \right) < 0 \Leftrightarrow x \ne \frac{1}{4}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\backslash \left\{ {\frac{1}{4}} \right\}\)
e) \(2{x^2} + x + 3 < 0\)
Ta có \(\Delta = {1^2} - 4.2.3 = - 23 < 0\) và có \(a = 2 > 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(2{x^2} + x + 3\) mang dấu “-” là \(\emptyset \)
Vậy tập nghiệm của bất phương trình \(2{x^2} + x + 3 < 0\) là \(\emptyset \)
g) \( - 3{x^2} + 4x - 5 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + 4x - 5\) có \(\Delta ' = {2^2} - \left( { - 3} \right).\left( { - 5} \right) = - 11 < 0\) và có \(a = - 3 < 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( - 3{x^2} + 4x - 5\) mang dấu “-” là \(\mathbb{R}\)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 4x - 5 < 0\) là \(\mathbb{R}\)

mình sẽ trả lời câu 1 thôi nha
TH1:|x-2|=0
th1:x-2=0=>x=2
th2:x-2=-0 x =-0+2 x=2
TH2:|x+5|=0
th1:x+5=0 x =0-5=-5
th2:x+5=-0 x =-0-5 x=-0+-5=-5
cậu tư suy ra nhé!^^

1) \(\left(x+2\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x+2=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\)
Vậy tập nghiệm \(S=\left\{-2;3\right\}\)
2) \(\left(2x+3\right)\left(-x+7\right)=0\Leftrightarrow\left[{}\begin{matrix}2x+3=0\\-x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-3}{2}\\x=7\end{matrix}\right.\)
Vậy...
3) \(\left(x-1\right)\left(x+5\right)\left(-3x+8\right)=0\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+5=0\\-3x+8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-5\\x=\dfrac{8}{3}\end{matrix}\right.\)
Vậy...
4) \(x\left(x^2-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\pm1\end{matrix}\right.\)
Vậy...
Kết quả hai phép tính bằng 0 nha
hok tốt
0x0=0
1x0=0
Hok tốt!!!