Cho tam giác ABCcos AB=AC.Tia phân giác của góc A cắt BC tại D
A Chứng minh:D là trung điểm của BC
b Chứng minh:AD vuông góc với BC
c Lấy E thuộc AB,F thuộc AC sao cho BE=CF.Chứng minh rằng DA là phân giác của EDF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD
Suy ra: \(\widehat{ADB}=\widehat{ADC}\)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
hay AD\(\perp\)BC
b: Ta có: AE+EB=AB
AF+FC=AC
mà EB=FC
và AB=AC
nên AE=AF
Xét ΔAED và ΔAFD có
AE=AF
\(\widehat{EAD}=\widehat{FAD}\)
AD chung
Do đó: ΔAED=ΔAFD
Suy ra: \(\widehat{EDA}=\widehat{FDA}\)
hay DA là tia phân giác của \(\widehat{EDF}\)

Lời giải:
1. Xét tam giác $ABD$ và $ACD$ có:
$AB=AC$
$\widehat{BAD}=\widehat{CAD}$ (do $AD$ là tia phân giác $\widehat{BAC}$)
$AD$ chung
$\Rightarrow \triangle BAD=\triangle CAD$ (c.g.c)
$\Rightarrow \widehat{ADB}=\widehat{ADC}$
Mà $\widehat{ADB}+\widehat{ADC}=180^0$
$\Rightarrow \widehat{ADB}=\widehat{ADC}=180^0:2=90^0$
$\Rightarrow AD\perp BC$
2.
$AB=AC$
$BE=CF$
$\Rightarrow AB-BE=AC-CF$ hay $AE=AF$
Xét tam giác $AED$ và $AFD$ có:
$AD$ chung
$AE=AF$
$\widehat{EAD}=\widehat{FAD}$
$\Rightarrow \triangle AED=\triangle AFD$ (c.g.c)
$\Rightarrow \widehat{EDA}=\widehat{FDA}$
$\Rightarrow DA$ là tia phân giác $\widehat{EDF}$
1: Xét ΔADB và ΔADC có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔADB=ΔADC
=>\(\widehat{ADB}=\widehat{ADC}\)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
=>AD\(\perp\)BC
2: Ta có: AE+EB=AB
AF+FC=AC
mà EB=FC và AB=AC
nên AE=AF
Xét ΔEAD và ΔFAD có
AE=AF
\(\widehat{EAD}=\widehat{FAD}\)
AD chung
Do đó: ΔEAD=ΔFAD
=>\(\widehat{EDA}=\widehat{FDA}\)
=>DA là phân giác của góc EDF

a) tam giác ABC có:
AB=AC => tam giác ABC cân tại A
Lại có: AD là đường phân giác của tam giác TG ABC
=> AD cũng là đường cao của tam giác ABC
b) xét tam giác EAD và tam giác ADF ta có:
AD chung
góc EAD = FDA ( AD là đpg)
AE =AF ( AB -BE=AC-FC)
=> TG EAD =TG ADF(cdc)
=> góc EDA=góc ADC(2 góc tương ứng)
mà AD nằm giữa 2 góc
=>...
a: Ta có ΔABC cân tại A
mà AD là đường phân giác ứng với cạnh đáy BC
nên AD⊥BC
b: Ta có: AE+BE=AB
AF+FC=AC
mà BE=CF
và AB=AC
nên AE=AF
Xét ΔAED và ΔAFD có
AE=AF
Góc EAD=góc FAD
AD chung
Do đó: ΔAED = ΔAFD
Suy ra: Góc EAD = góc FDA
hay DA là tia phân giác của góc EDF

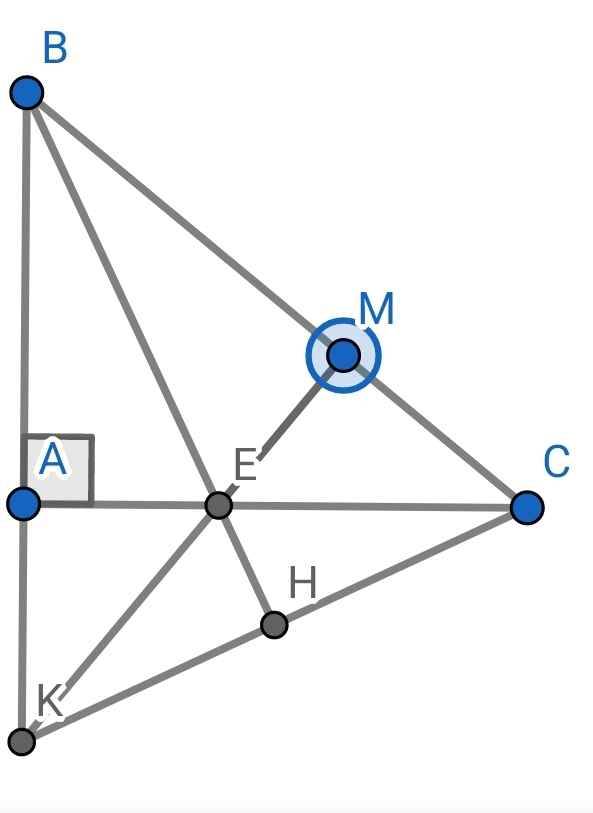
a) Xét ∆ABE và ∆MBE có:
BE chung
góc ABE = góc MBE (BE là phân giác của góc ABC)
AB = BM
⇒∆ABE = ∆MBE (c-g-c)
⇒góc BAE = góc BME (hai góc tương ứng)
⇒ME vuông góc BC
b) Do ∆ABE = ∆MBE (cmt)
⇒AE = ME (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆AEK và ∆MEC có:
AE = ME (cmt)
góc AEK = góc MEC (đối đỉnh)
⇒∆AEK = ∆MEC (cạnh góc vuông - góc nhọn kề)
⇒EK = EC (hai cạnh tương ứng)
AK = MC (hai cạnh tương ứng)
Lại có: BK = BA + AK
BC = BM + MC
⇒BK = BC
c) Gọi H là giao điểm của BE và CK
Xét ∆BHK và ∆BHC có:
BK = BC (cmt)
góc HBK = góc HBC (do BE là tia phân giác của góc ABC)
BH chung
⇒∆BHK = ∆BHC (c-g-c)
⇒góc BHK = góc BHC (hai góc tương ứng)
Mà góc BHK + góc BHC = 180⁰ (kề bù)
⇒góc BHK = góc BHC = 180⁰ : 2 = 90⁰
⇒BH vuông góc KC
Hay BE vuông góc KC