Phép đối xứng tâm I (1;1) biến đường thẳng d' : x'+y'-2=0 thành đường thẳng d có phương trình là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 8 2021
Phương trình đường tròn (C) : (x + 1)2 + (y - 3)2 = 2 + 1 + 9 = 12
Vậy (C) có tâm A(-1 ; 3) và bán kính R = \(2\sqrt{3}\)
a, Phép đối xứng qua tâm O biết (C) thành một đường tròn có tâm có tọa độ là (1 ; -3) và bán kính vẫn bằng \(2\sqrt{3}\)
Phương trình đường tròn đó là : (x - 1)2 + (y + 3)2 = 12
b, Đối xứng qua tâm I (2 ; -3) biến A thành B và I là trung điểm của AB và bán kính đường tròn mới vẫn bằng \(2\sqrt{3}\). TÌm tọa độ I là được
CM
15 tháng 1 2018
Gọi tam giác A'B'C' là ảnh của tam giác ABC qua phép biến hình trên.
(e)Phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Oy và phép vị tự tâm O tỉ số k = -2
+) Qua phép đối xứng qua trục Oy biến tam giác ABC thành tam giác A 1 B 1 C 1
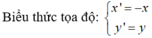
Do đó, tọa độ A 1 - 1 ; 1 ; B 1 0 ; 3 v à C 1 - 2 ; 4 .
+) Qua phép vị tự tâm O tỉ số k = -2 biến tam giác A 1 B 1 C 1 thành tam giác A 2 B 2 C 2
Biểu thức tọa độ :
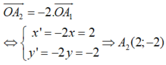
Tương tự; B 2 0 ; - 6 v à C 2 4 ; - 8
Vậy qua phép đối xứng trục Oy và phép vị tự tâm O tỉ số k = -2, biến các điểm A, B, C lần lượt thành
A 2 2 ; - 2 ; B 2 0 ; - 6 v à C 2 4 ; - 8 .
CM
7 tháng 4 2019
Đáp án B
I là trung điểmđoạn MM’ Áp dụng công thức tọa độ trung điểm để tính
CM
17 tháng 5 2019
Đáp án B
x M + x M ' = 2 x I y M + y M ' = 2 y I
=> M’(–3;–6)
CM
4 tháng 5 2019
Đáp án A
C : x 2 + y 2 = 1 O 0 ; 0 , R = 1 Đ I O = O ' ⇒ O ' 2 ; 0 C ' : x − 2 2 + y 2 = 1
CM
15 tháng 5 2017
+ Gọi (I1; R1) là ảnh của (I; 2) qua phép vị tự tâm O, tỉ số 3.
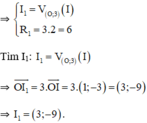
+ Gọi (I2; R2) là ảnh của (I1; R1) qua phép đối xứng trục Ox
⇒ R2 = R1 = 6.
I2 đối xứng với I1 qua Ox ⇒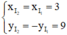 
⇒ I2(3; 9)
Vậy (I2; R2) chính là ảnh của (I; 2) qua phép đồng dạng trên và có phương trình: (x – 3)2 + (y – 9)2 = 36.
Lấy \(M'\left(x';y'\right)\in d'\) \(\Rightarrow D_I\left(M'\right)=M\) có tọa độ:
\(\left\{{}\begin{matrix}x=2-x'\\y=2-y'\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x'=2-x\\y'=2-y\end{matrix}\right.\)
Thay vào pt (d') ta được:
\(2-x+2-y-2=0\Leftrightarrow x+y-2=0\)