Ai làm giúp em với ạ
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi H và K lần lượt là trung điểm của SA và SC, G là trọng tâm của tầm giác ABC.
a, Tìm giao tuyến của (GHK) và (ABCD)
b, Tìm giao điểm M của SD và (GHK)
c, Gọi E là trung điểm HK. Chứng minh G,E,M thẳng hàng




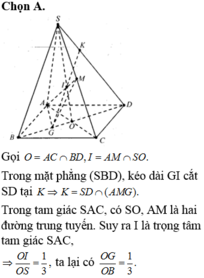
Qua G kẻ đường thẳng song song AC lần lượt cắt AD, AB, BC tại E, F, N.
\(\Rightarrow FN\) là giao tuyến của (GHK) và (ABCD)
Nối EH kéo dài cắt SD tại M \(\Rightarrow M\) là giao điểm SD và (NHK)
c/ Gọi P là giao điểm của FN kéo dài và CD
Ta có \(AC//EP\) \(\Rightarrow\Delta DAC\sim\Delta DEP\), mà BD qua trung điểm của AC \(\Rightarrow BD\) qua trung điểm của EP \(\Rightarrow G\) là trung điểm EP
\(HK//EP\Rightarrow\Delta MEP\sim\Delta MHK\)
Mà MG qua trung điểm của EP \(\Rightarrow\) MG qua trung điểm của HK hay G,M,E thẳng hàng