chứng minh rằng:29-1=30
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Biểu thị phép tính trên bằng các số La Mã, ta có:
29 = XXIX
1 = I
=> 29 - 1 = XXIX - I = XXX
=> 29 - 1 = 30 ( ĐPCM )
Hk tốt ~
Biểu thị phép tính trên bằng số La Mã, ta có:
29= XXIX; 1= I; 30= XXX
29-1= XXIX- I = XXX
=> 29-1=30 (đpcm)
Chúc bạn hok tốt (^_^)



\(S=2^1+2^2+2^3+2^4+2^5+2^6+..+2^{28}+2^{29}+2^{30}\)
\(S=2.\left(1+2+2^2\right)+2^4.\left(1+2+2^2\right)+...+2^{28}.\left(1+2+2^2\right)\)
\(S=\left(1+2+2^2\right).\left(2+2^4+...+2^{28}\right)\)
\(S=7.\left(2+2^4+...+2^{28}\right)\)
⇒ \(S⋮7\) ( điều phải chứng minh )

Ta có : A = 1 + 2 + 22 + ..... + 230
=> 2A = 2 + 22 + ..... + 231
=> 2A - A = 231 - 1
=> A = 231 - 1 (đpcm)
\(A=1+2+2^2+.......+2^{29}+2^{30}\)
\(2A=2.\left(1+2+2^2+........+2^{29}+2^{30}\right)\)
\(2A=2+2^2+2^3+......+2^{30}+2^{31}\)
\(2A-A=\left(2+2^2+2^3+.....+2^{30}+2^{31}\right)-\left(1+2+2^2.....+2^{29}+2^{30}\right)\)
\(A=2^{31}-1\)
\(\Rightarrow A=1+2+2^2+......+2^{29}+2^{30}=2^{31}-1\)

\(A=3+3^2+3^3+...+3^{28}+3^{29}+3^{30}\)
\(A=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{29}+3^{30}\right)\)
\(A=1\left(3+3^2\right)+3^2\left(3+3^2\right)+....+3^{28}\left(3+3^2\right)\)
\(A=\left(1+3^2+...+3^{28}\right)\left(3+3^2\right)\)
\(A=13\left(1+3^2+...+3^{28}\right)⋮13\left(đpcm\right)\)
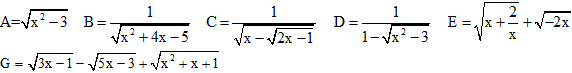 Mn giúp em với ;-;
Mn giúp em với ;-;
29 -1 =30 khi mà phép tính sai ôke
Bạn viết sai đầu bài rồi