Gọi S là tập tất cả các giá trị nguyên của tham số m để phương trình 4x -m.2x + (10-m) =0 có hai nghiệm phân biệt. Tính tổng giá trị các phần tử của S.
A.45 B.42 C.35 D.52
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 2 2018
Đáp án B
Phương trình (1) có hai nghiệm dương phân biệt khi và chỉ khi phương trình (2) có hai nghiệm phân biệt lớn hơn 1.
Bảng biến thiên của hàm số y = t 2 - 10 t
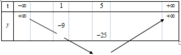
Phương trình (2) có hai nghiệm phân biệt lớn hơn 1 khi và chỉ khi -25< m < -9
Vậy S = {-24;-23;...;-10} và n(S) =15
Đặt \(2^x=t>0\Rightarrow t^2-mt+10-m=0\) (1)
Để pt đã cho có 2 nghiệm pb thì (1) có 2 nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=m^2-4\left(10-m\right)>0\\S=m>0\\P=10-m>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< -2-2\sqrt{11}\\m>-2+2\sqrt{11}\end{matrix}\right.\\0< m< 10\end{matrix}\right.\)
\(\Rightarrow m=\left\{5;6;7;8;9\right\}\) \(\Rightarrow\sum m=35\)