cho a/b tìm x y để a+x/b+y = a/b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



A=B
=>x=2
=>A={2;5}; B={5;2}; C={2;y;5}
B=C
=>y phải trùng với 2 hoặc 5
=>\(y\in\left\{2;5\right\}\)

a: Thay x=-1 và y=0 vào (d), ta được:
\(3a-1+5=0\)
\(\Leftrightarrow3a=-4\)
hay \(a=-\dfrac{4}{3}\)
b: Thay x=2 và y=10 vào (d), ta được:
\(3a+2+5=10\)
\(\Leftrightarrow3a=3\)
hay a=1

a, A = {x ∈ ¥|5<x<11}
b, 9 ∈ A; x ∉ A; y ∈ B
c, A = B <=> x = 6; y = 8 hoặc x = 8; y = 6
Nhận xét: Vì thứ tự liệt kê các phần tử không quan trọng nên ở câu c ta có 2 đáp số.

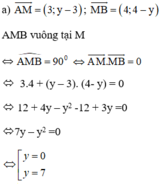
Vậy với M(5; 7) hoặc M(5; 0) thì tam giác ABM vuông tại M.

Vậy P(-5; 2)

Để \(A = B\)
\(\begin{array}{l} \Leftrightarrow \left\{ {5;x} \right\} = \left\{ {2;5} \right\}\\ \Leftrightarrow x = 2\end{array}\)
Tương tự, ta có:
\(\begin{array}{l}A = C \\\Leftrightarrow \left\{ {2;y} \right\} = \left\{ {2;5} \right\} \\ \Leftrightarrow y = 5\end{array}\)
Vậy \(x = 2;y = 5\) thì \(A = B = C\).
Ta có:
\(\frac{a+x}{b+y}=\frac{a}{b}\)
\(\Leftrightarrow b\left(a+x\right)=a\left(b+y\right)\)
\(\Leftrightarrow ba+bx=ab+ay\)
\(\Leftrightarrow bx=ay\)
\(\Leftrightarrow\frac{b}{a}=\frac{y}{x}\)
\(\Leftrightarrow\frac{a}{b}=\frac{x}{y}\)
Vậy ......