Tìm x \(\in Q\)để biểu thức P = 2x2 + 5x nhận giá trị dương
Helpp me :(
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) 3x - 2
Ta có: 3x - 2 > 0
=> 3x > 2
=> x > \(\frac{2}{3}\)
Vậy khi x > \(\frac{2}{3}\)thì biểu thức 3x-2 nhận giá trị dương
2) x2 - 5x
Ta có: x2 - 5x > 0
=> x.(x-5) > 0
=> x>0 và x - 5 > 0 => x > 0 và x > 5
=> x > 5 và x < 0
x < 0 và x - 5 < 0 => x < 0 và x < 5
Vậy x > 5 hoặc x < 0

Giá trị của biểu thức xác định khi mỗi giá trị của phân thức trong biểu thức đều được xác định.
Khi đó điều kiện xác định:
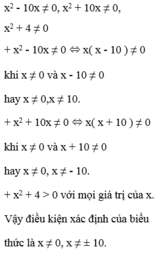

Giá trị của biểu thức xác định khi mỗi giá trị của phân thức trong biểu thức đều được xác định.
Khi đó điều kiện xác định:


b) Vậy C = 2 ⇒ (2/x) = 2
⇒ x = 1(thỏa mãn các điều kiện trên).

a: \(x^2-5x+10\)
\(=x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}+\dfrac{15}{4}\)
\(=\left(x-\dfrac{5}{2}\right)^2+\dfrac{15}{4}>0\forall x\)
b: \(2x^2+8x+15\)
\(=2\left(x^2+4x+\dfrac{15}{2}\right)\)
\(=2\left(x^2+4x+4+\dfrac{7}{2}\right)\)
\(=2\left(x+2\right)^2+7>0\forall x\)

Bài 1:
a) Ta có: \(P=1+\dfrac{3}{x^2+5x+6}:\left(\dfrac{8x^2}{4x^3-8x^2}-\dfrac{3x}{3x^2-12}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{8x^2}{4x^2\left(x-2\right)}-\dfrac{3x}{3\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{4}{x-2}-\dfrac{x}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\dfrac{4\left(x+2\right)-x-\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}\cdot\dfrac{\left(x-2\right)\left(x+2\right)}{4x+8-x-x+2}\)
\(=1+3\cdot\dfrac{\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=1+\dfrac{3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{\left(x+3\right)\left(2x+10\right)+3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+10x+6x+30+3x-6}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+19x-6}{\left(x+3\right)\left(2x+10\right)}\)

a) x ≠ 2 và x ≠ 0
b) Rút gọn được Q = x + 1 2 x
c) Thay x = 2017 (TMĐK) vào Q ta được Q = 1009 2017

P=\(2x^2+5x\)
=\(2\left(x^2+\frac{5}{2}x\right)\)
=\(2\left(x^2+2x.\frac{5}{4}+\frac{25}{16}-\frac{25}{16}\right)\)
= \(2\left(x+\frac{5}{4}\right)^2-\frac{25}{8}\)
de P nhan gia tri duong thi
\(2\left(x+\frac{5}{4}\right)^2>\frac{25}{8}\)
<=> \(\left(x+\frac{5}{4}\right)^2>\frac{25}{16}\)
<=> \(\orbr{\begin{cases}x+\frac{5}{4}>\frac{5}{4}\\x+\frac{5}{4}< \frac{-5}{4}\end{cases}\Leftrightarrow\orbr{\begin{cases}x>0\\x< \frac{-5}{2}\end{cases}}}\)
vay voi x>0 hoac x< -5/2 thi P dat gia tri duong
Chuc ban hoc tot