Cho x, y thay đổi thỏa mãn 0<x<1, 0<y<1.
Tìm GTLN của biểu thức: P=\(x+y+x\sqrt{1-y^2}+y\sqrt{1-x^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BM
0
CM
28 tháng 12 2019
Đáp án D
Phương pháp giải:
Đặt ẩn phụ, đưa về hàm một biến, dựa vào giả thiết để tìm điều kiện của biến
Lời giải:
Từ giả thiết chia cả 2 vế cho x2y2 ta được :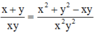 
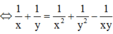
Đặt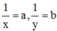 
ta có 
Khi đó 
Ta có 
mà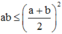 
nên 
Dấu đẳng thức xảy ra khi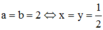 
. Vậy Mmax = 16
FF
13 tháng 8 2016
1. Đặt x = √2.cosα và y = √2.sinα (với α trên [0,3π/2])
Ta có: P = 4√2(sinα + cosα)(1 - sinαcosα) - 6sinαcosα
Đặt t = sinα + cosα = √2.sin(α + π/4) có |t| ≤ √2, nên sinαcosα = (t^2 - 1)/2
suy ra P = -2√2.t^3 - 3t^2 + 6√2.t + 3.
Đến đây bạn áp dụng P' = 0 rồi xét các gtrị cực trị.
2. Đặt x = cosα và y = sinα (với α trên [0,3π/2])
Biến đổi P = (6sin2α + cos2α + 1) / (3 + sin 2α - cos 2α)
Mặt khác lại có (cos2α)^2 + (sin 2α)^2 = 1.
Ta áp dụng P' = 0 tiếp.
CM
9 tháng 4 2018
Ta có
P = x 2 4 + 8 y + y 2 1 + x = x 2 4 + 8 y + 2 y 2 4 + 4 x ≥ x + 2 y 2 8 + 4 x + 2 y
Dấu “=” xảy ra khi x = 2y
Đặt t = x + 2y; t ≥ 8 . Khi đó P ≥ t 2 8 + 4 t
Xét hàm số f t = t 2 8 + 4 t , t ∈ [ 8 ; + ∞ )
Suy ra f(t) đồng biến trên [ 8 ; + ∞ ) nên f t ≥ f 8 = 8 5 Vậy m a x P = 8 5 ⇔ x = 4 ; y = 2
Đáp án A