3√x + 1 = 40
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LH
14
22 tháng 5 2018
ta có: \(S=1+1.2+2.3+3.4+...+38.39+39.40+40\)
\(\Rightarrow3S=3+1.2.3+2.3.3+3.4.3+...+38.39.3+39.40.3+40.3\)
\(3S=3+1.2.\left(3-0\right)+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+38.39.\left(40-37\right)\)
\(+39.40.\left(41-38\right)+120\)
\(3S=3+1.2.3+2.3.4-1.2.3+3.4.5-2.3.4+...+38.39.40-37.38.39\)
\(+39.40.41-38.39.40+120\)
\(3S=\left(3+1.2.3+2.3.4+3.4.5+...+39.40.41+120\right)-\left(1.2.3+2.3.4+...+38.39.40\right)\)
\(3S=3+39.40.41+120\)
\(\Rightarrow S=\frac{3+39.40.41+120}{3}\)
\(S=21361\)
LH
22 tháng 5 2018
Mình tìm ra kết quả là 21443 . Sai thì các bn cứ k sai cho mình nhé . Mình sẽ rút kinh nhiệm . Còn bn nào thông minh có thể giúp mình được không . Mình sẽ k .
Rút gọn các biểu thức 
DH
5 tháng 7 2017
\(A=\left(x+1\right)^3-\left(x+3\right)^2\left(x+1\right)+4x^2+8\)
\(A=x^3+3x^2+3x+1-\left(x^2+6x+9\right)\left(x+1\right)+4x^2+8\)
\(A=x^3+3x^2+3x+1-\left(x^3+6x^2+9x+x^2+6x+9\right)+4x^2+8\)
\(A=x^3+3x^2+3x+1-x^3-6x^2-9x-x^2-6x-9+4x^2+8\)
\(A=\left(x^3-x^3\right)+\left(3x^2-6x^2-x^2+4x^2\right)+\left(3x-9x-6x\right)+\left(1-9+8\right)\)
\(A=-12x\)
\(B=\left(x-2\right)\left(x^2+2x+4\right)-\left(x+1\right)^3+3\left(x-1\right)\left(x+1\right)\)
\(B=x^3+2x^2+4x-2x^2-4x-8-\left(x^3+3x^2+3x+1\right)+3\left(x^2-1\right)\)
\(B=x^3+2x^2+4x-2x^2-4x-8-x^3-3x^2-3x-1+3x^2-3\)
\(B=\left(x^3-x^3\right)+\left(2x^2-2x^2-3x^2+3x^2\right)+\left(4x-4x-3x\right)+\left(-8-3-1\right)\)
\(B=-3x-12\)
Câu C tương tự.
Chúc bạn học tốt!!!
HL
5 tháng 7 2017
A = \(\left(x+1\right)^3-\left(x+3\right)^2.\left(x+1\right)+4x^2+8\)
A = \(\left(x+1\right)\left(x+1-x-3\right)\left(x+1+x+3\right)+4x^2+8\)
A = \(\left(x+1\right).\left(-2\right).\left(2x+4\right)+4x^2+8\)
A = \(\left(-2\right)\left(2x^2+4x+2x+4\right)+4x^2+8\)
A = \(\left(-2\right)\left(2x^2+6x+4\right)+4x^2+8\)
A = \(-4x^2-12x-8+4x^2+8=-12x\)
b) B = \(\left(x-2\right)\left(x^2+2x+4\right)-\left(x+1\right)^3+3\left(x-1\right)\left(x+1\right)\)
B = \(x^3-8-\left(x+1\right)\left(x^2+2x+1+3x-3\right)\)
B = \(x^3-8-\left(x+1\right)\left(x^2+5x-2\right)\)
B = \(x^3-8-x^3-5x^2+2x-x^2-5x+2\)
B = \(-6x^2-3x-6\)
6 tháng 1 2022
e: =>-40+3+33+40-x=47
=>36-x=47
=>x=-11
f: =>x(x-3)(11-x)(11+x)=0
hay \(x\in\left\{0;3;11;-11\right\}\)
g: =>-62-38-x+2x=-100
=>x-100=-100
hay x=0
6 tháng 1 2022
i: =>x-12-2x-31=6
=>-x-43=6
=>x+43=-6
hay x=-49
h: =>(x+1)=0
=>x=-1
f: =>x(x-3)(x+11)(x-11)=0
hay \(x\in\left\{0;3;-11;11\right\}\)
MV
14 tháng 5 2017
\(\dfrac{3}{1}+\dfrac{3}{3}+\dfrac{3}{6}+...+\dfrac{3}{x\cdot\left(x+1\right):2}=\dfrac{2015}{336}\\ \dfrac{6}{2}+\dfrac{6}{6}+\dfrac{6}{12}+...+\dfrac{6}{x\cdot\left(x+1\right)}=\dfrac{2015}{336}\\ 6\cdot\dfrac{1}{2}+6\cdot\dfrac{1}{6}+6\cdot\dfrac{1}{12}+...+6\cdot\dfrac{1}{x\cdot\left(x+1\right)}=\dfrac{2015}{336}\\ =6\cdot\left(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{x\cdot\left(x+1\right)}\right)=\dfrac{2015}{336}\\ 6\cdot\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{x\cdot\left(x+1\right)}\right)=\dfrac{2015}{336}\\ 6\cdot\left(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{x}-\dfrac{1}{x+1}\right)=\dfrac{2015}{336}\\ 6\cdot\left(1-\dfrac{1}{x+1}\right)=\dfrac{2015}{336}\\ 1-\dfrac{1}{x+1}=\dfrac{2015}{336}:6\\ 1-\dfrac{1}{x+1}=\dfrac{2015}{2016}\\ \dfrac{1}{x+1}=1-\dfrac{2015}{2016}\\ \dfrac{1}{x+1}=\dfrac{1}{2016}\\ \Rightarrow x+1=2016\\ x=2016-1\\ x=2015\)
12 tháng 2 2022
Bài 1:
\(P=3^x\left(3+3^2+3^3+3^4\right)+...+3^{x+96}\left(3+3^2+3^3+3^4\right)\)
\(=120\left(3^x+...+3^{x+96}\right)⋮120\)
DN
0
LV
0
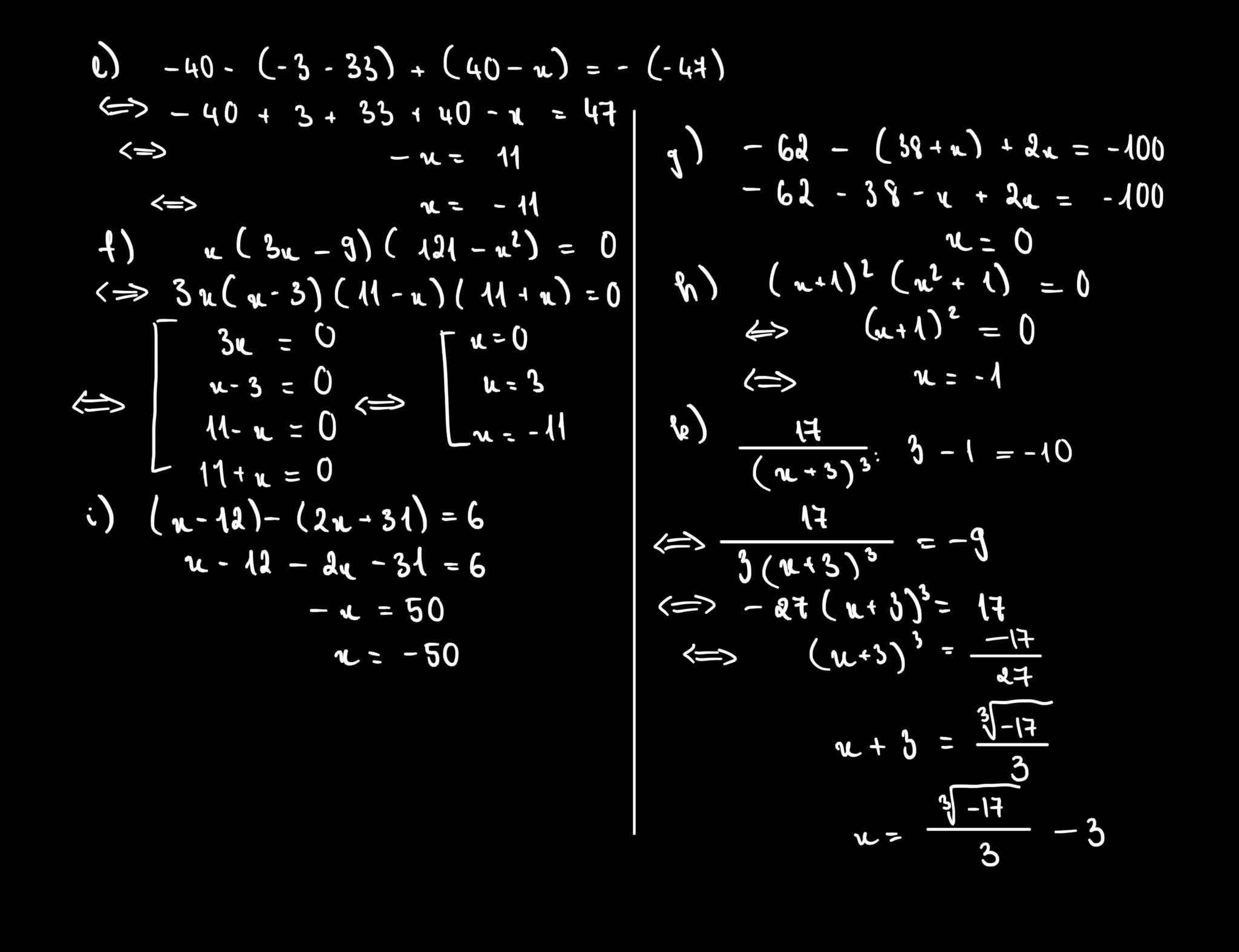
\(3\sqrt{x}+1=40\)
\(ĐKXĐ:x\ge0\)
\(pt\Leftrightarrow3\sqrt{x}=39\)
\(\Leftrightarrow\sqrt{x}=13\)
\(\Leftrightarrow x=169\)
\(3\sqrt{x}+1=40\left(ĐK:x\ge0\right)\)
\(\Leftrightarrow3\sqrt{x}=39\)
\(\Leftrightarrow\sqrt{x}=39:3=13\)
\(\Leftrightarrow x=13.13=169\)
Vậy x = 169