bài 1: Cho tam giác ABC vuông ở A, góc C = 30 độ. cạnh BC = 10 cm.
a, Tính AB và AC
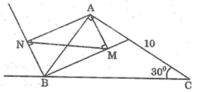
b, Từ A kẻ AM và AN lần lượt vuông góc với các đường phân giác trong và ngoài của góc B. Chứng minh MN // BC và MN = AB
hộ mình với nhé mình đang gấp :)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 3 2019
Suy ra: MN // BC (có cặp góc so le trong bằng nhau)
Vì AMBN là hình chữ nhật nên AB = MN
30 tháng 7 2020
a. Trong tam giác vuông ABC, ta có :
\(AB=BC.\sin\widehat{C}=10.\sin30^o=10.\frac{1}{2}=5\left(cm\right)\)
\(AC=BC.\cos\widehat{C}=10.\cos30^o=10.\frac{\sqrt{3}}{2}=5\sqrt{3}\left(cm\right)\)
b)
Ta có : \(BM\perp BN\)( tính chất 2 góc kề bù ) \(\Rightarrow\widehat{MBN}=90^o\left(1\right)\)
\(AM\perp BM\left(gt\right)\Rightarrow\widehat{AMB}=90^o\left(2\right)\)
\(AN\perp BN\left(gt\right)\Rightarrow\widehat{ANB}=90^o\left(3\right)\)
Từ (1) (2) và (3) , suy ra : tứ giác AMBN là hình chữ nhật
\(\Rightarrow\Delta AMB=\Delta NBM\left(c.g.c\right)\)
\(\Rightarrow\widehat{ABM}=\widehat{NMB}\)
Mà \(\widehat{ABM}=\widehat{MBC}\left(gt\right)\)
\(\Rightarrow\widehat{NMB}=\widehat{NBC}\)
Suy ra: MN // BC (có cặp góc so le trong bằng nhau)
Vì AMBN là hình chữ nhật nên AB = MN
30 tháng 7 2020
)): gửi cả câu c) rồi mà cuối cùng lại 0 có , làm lại câu c) sang bên này :>
c)
Tam giác ABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^o\)
\(\Rightarrow\widehat{B}=90^o-\widehat{C}=90^o-30^o=60^o\)
\(\Rightarrow\widehat{ABM}=\frac{1}{2}\widehat{B}=\frac{1}{2}.60^o=30^o\)
Xét 2 tam giác ABC và MAB ,, ta có :
\(\widehat{BAC}=\widehat{AMB}=90^o\)
\(\widehat{ACB}=\widehat{ABM}=90^o\)
\(\Rightarrow\Delta ABC~\Delta MAB\left(g.g\right)\)
=> Tỉ số đồng dạnh \(k=\frac{AB}{BC}=\frac{5}{10}=\frac{1}{2}\)
CM
25 tháng 5 2017
a, HS tự làm
b, Chú ý hai đường phân giác trong và ngoài tại một đỉnh vuông góc nhau
c, Chú ý BM là phân giác góc ABC. Từ đó tính được số đo các góc của tam giác MAB và suy ra ĐPCM
Chú ý Hai tam giác MAB và ABC đều là các tam giác nửa đều
Từ đó tính được tỉ số đồng dạng là 1/2
Ai giải hộ đi -_- mình xin các bạn