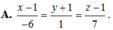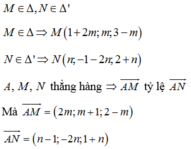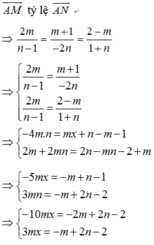Cho hai điểm A(x1;y1) và B(x2;y2) với x1\(\ne\)x2; y1\(\ne\)y2 . Chứng minh rằng nếu đường thẳng y=ax+b đi qua A và B thì \(\frac{y-y1}{y2-y1}\) = \(\frac{x-x1}{x2-x1}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+ Đạo hàm : y’ = 4/3.x3-28/3. x
y 2 - y 1 = 8 ( x 2 - x 1 ) ⇔ y 2 - y 1 x 2 - x 1 = 8
Vậy tiếp tuyến của (C) tại A có hệ số góc bằng 8.
+ Xét phương trình y' = 8
⇔ 4 3 x 3 - 28 3 x = 8 ⇔ 4 x 3 - 28 x - 24 = 0
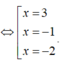
+) Với x= 3 thì A( 3; -15) nên phương trình tiếp tuyến của (C) tại A là y = 8(x-3) - 15 ( d 1 )
Phương trình hoành độ giao điểm của (C) và ( d 1 ) là
8 ( x - 3 ) - 15 = 1 3 x 4 - 14 3 x 2 ⇔ ( x - 3 ) 2 ( x 2 + 6 x + 13 ) = 0 ⇔ x = 3 .
Vậy A(3; -15) loại.
+) Với x= -2 thì A(-2; -40/3) . phương trình tiếp tuyến của (C) tại A là y = 8(x+2) - 40/3 ( d 2 )
Phương trình hoành độ giao điểm của ( C) và ( d 2 ) là
8 ( x + 2 ) - 40 3 = 1 3 x 4 - 14 3 x 2 ⇔ ( x + 2 ) 2 ( x 2 - 4 x - 2 ) = 0
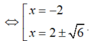
Vậy A( -2; -40/3) thỏa mãn.
+) Với x= -1 thì A( -2; -13/ 3) nên phương trình tiếp tuyến của C tại A là
y = 8(x+1) - 13/3 (d3)
Phương trình hoành độ giao điểm của C và (d3) là:
8 ( x + 1 ) - 13 3 = 1 3 x 4 - 14 3 x 2 ⇔ ( x + 2 ) 2 ( x 2 - 2 x - 11 ) = 0

Vậy A( -1; -13/3) thỏa mãn.
Vậy có tất cả 2 điểm A thỏa mãn yêu cầu bài toán.
Chọn B.

Đáp án B
+ Hai dao động lệch pha nhau 0,25π và hai thời điểm lệch nhau nhau một lượng 0,125T → li độ tương ứng vuông pha nhau → a 2 + b 2 = A 2 .

a: khi m=1 thì pt sẽ là:
x^2-4x-5=0
=>x=5; x=-1
b: |x1|-|x2|=-2022
=>x1^2+x2^2-2|x1x2|=2022^2
=>(x1+x2)^2-2x1x2-2|x1x2|=2022^2
=>(2m+2)^2-2|-5|-2*(-5)=2022^2
=>(2m+2)^2=2022^2
=>2m+2=2022 hoặc 2m+2=-2022
=>m=1010 hoặc m=-1012

a: y=mx+3
Thay x=1 và y=0 vào (d), ta được:
m+3=0
=>m=-3
b: PTHĐGĐ là:
x^2-mx-3=0
Vì a*c=-3<0
nên (P) luôn cắt (d) tại hai điểm phân biệt
|x1-x2|=2
=>\(\sqrt{\left(x_1-x_2\right)^2}=2\)
=>\(\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=2\)
=>\(\sqrt{m^2-4\left(-3\right)}=2\)
=>m^2+12=4
=>m^2=-8(loại)
=>KO có m thỏa mãn đề bài

a: Phương trình hoành độ giao điểm là:
\(x^2-mx+m-1=0\)
\(\text{Δ}=\left(-m\right)^2-4\left(m-1\right)=m^2-4m+4=\left(m-2\right)^2\)
Để (P) và (d) cắt nhautại hai điểm phân biệt thì m-2<>0
hay m<>2
b: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_1=9x_2\\x_1+x_2=-m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{-1}{10}m\\x_1=\dfrac{-9}{10}m\end{matrix}\right.\)
Ta có: \(x_1x_2=m-1\)
\(\Leftrightarrow m^2\cdot\dfrac{9}{100}-m+1=0\)
\(\Leftrightarrow9m^2-100m+100=0\)
\(\text{Δ}=\left(-100\right)^2-4\cdot9\cdot100=6400>0\)
Do đó: PT có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}m_1=\dfrac{100-80}{18}=\dfrac{20}{18}=\dfrac{10}{9}\\m_2=\dfrac{100+80}{18}=10\end{matrix}\right.\)

Xét pt hoành độ gđ của (P) và (d) có:
\(x^2=\left(2m-1\right)x+8\)
\(\Leftrightarrow x^2-\left(2m-1\right)x-8=0\) (*)
Có \(ac=-8< 0\) => pt luôn có hai nghiệm trái dấu
=> (d) luôn cắt (P) tại hai điểm pb có hoành độ trái dấu hay (d) luôn cắt (P) tại hai điểm phân biệt nằm về hai phía trục tung
Hoành độ gđ của A và B là hai nghiệm của pt (*) mà \(x_1< x_2\Rightarrow x_1< 0< x_2\)
Theo viet có: \(\left\{{}\begin{matrix}x_1+x_2=2m-1\\x_1x_2=-8\end{matrix}\right.\) (|)
Giả sử \(\dfrac{\left|x_1\right|}{\left|x_2\right|}=4\)
\(\Leftrightarrow\dfrac{-x_1}{x_2}=4\)\(\Leftrightarrow x_1+4x_2=0\) (||)
Từ (|), (||) có hệ: \(\left\{{}\begin{matrix}x_1+x_2=2m-1\\x_1+4x_2=0\\x_1x_2=-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{1-2m}{3}\\x_1=\dfrac{4\left(2m-1\right)}{3}\\x_1x_2=-8\end{matrix}\right.\)\(\Rightarrow\dfrac{\left(1-2m\right)}{3}.\dfrac{4\left(2m-1\right)}{3}=-8\) \(\Leftrightarrow\left(1-2m\right)^2=18\)
\(\Leftrightarrow m=\dfrac{1\pm\sqrt{18}}{2}\)
Vậy...