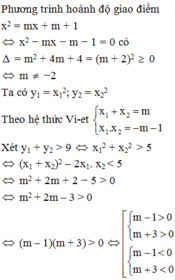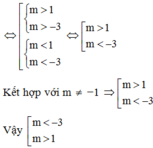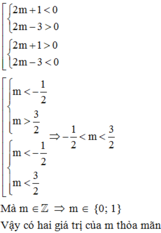Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Pt hoành độ giao điểm của (P) và (d) là: 2x2 = -x + 6 <=> 2x2 + x - 6 = 0
\(\Delta=1^2+4.6.1=25>0\)
=> pt có 2 nghiệm pb : x1 = -2; x2 = 3/2 (vì x1 < x2)
x1 = -2 => y1 = 2.(-2)2 = 8
x2 = 3/2 => y2 = 2. (3/2)2 = 9/2
Do đó: 4x2 + y1 = 4.3/2 + 8 = 14

PTHĐGĐ là;
x^2-3x-m^2+1=0
Δ=(-3)^2-4(-m^2+1)=4m^2-4+9=4m^2+5>0
=>Phương trình luôn có hai nghiệm phân biệt
TH1: x1>0; x2>0
=>x1+2x2=3
mà x1+x2=3
nên x1=1; x2=1
x1*x2=-m^2+1
=>-m^2+1=1
=>m=0
TH2: x1<0; x2>0
=>-x1+2x2=3 và x1+x2=3
=>x1=1; x2=2
x1*x2=-m^2+1
=>-m^2+1=2
=>-m^2-1=0(loại)
TH2: x1>0; x2<0
=>x1-2x2=0 va x1+x2=3
=>x1=2 và x2=1
x1*x2=-m^2+1
=>-m^2+1=2
=>-m^2=1(loại)
TH3: x1<0; x2<0
=>-x1-2x2=3 và x1+x2=3
=>x1=9 và x2=-6
x1*x2=-m^2+1
=>-m^2+1=-54
=>-m^2=-55
=>\(m=\pm\sqrt{55}\)

Phương trình hoành độ giao điểm của (P) và d: x 2 − m x + 2 = 0 (1)
P) cắt d tại hai điểm phân biệt A(x1;y1) và B(x2;y2) ⇔ (1) có hai nghiệm phân biệt
⇔ ∆ = m2 – 4.2 > 0 ⇔ m2 > 8 ⇔ m > 2 2 hoặc m<- 2 2
Khi đó x1, x2 là nghiệm của (1). Áp dụng định lí Vi–ét ta có x1 + x2 = m; x1x2 = 2.
Do A, B ∈ d nên y1 = mx1 – 2 và y2 = mx2 – 2.
Ta có:
y 1 + y 2 = 2 ( x 1 + x 1 ) − 1 < = > m x 1 − 2 + m x 2 − 2 = 2 ( x 1 + x 2 ) − 1 < = > ( m − 2 ) ( x 1 + x 2 ) − 3 = 0 < = > m ( m − 2 ) − 3 = 0 < = > m 2 − 2 m − 3 = 0
⇔ m = –1 (loại) hoặc m = 3 (thỏa mãn)
Vậy m = 3 là giá trị cần tìm.

a) Xét phương trình hoành độ giao điểm (d) và (P)
\(x^2 = 2(m+1)x - 4\)
\(<=> x^2 -2(m+1) + 4 = 0\) (1)
có \(\Delta' = [-(m+1)]^2 -4\)
\(\Delta' = (m+1)^2- 4\)
(d) và (P) cắt nhau tại hai điểm phân biệt
<=> Phương trình (1) có hai nghiệm phân biệt
<=> \(\Delta' \)> 0
<=> \((m + 1)^2 - 4 >0\)
<=> \((m+1)^2 >4\)
<=> \(\left[ \begin{array}{l}m+1 > 2\\m+1 <- 2\end{array} \right. \)
\(<=> \left[ \begin{array}{l}m > 1\\m < -3\end{array} \right. \)
b) Vì x1;x2 là hoành độ giao điểm của (d) và (P)
nên x1;x2 là hai nghiệm của phương trình (1)
Áp dụng hệ thức Viet có x1 + x2 = 2(m+1)
x1x2 = 4
Mà \(\sqrt{x_1} - \sqrt{x_2} = 2\)(x1;x2 \(\geq \) 0)
=> \((\sqrt{x_1} - \sqrt{x_2})^2 = 4\)
<=> x1 - 2x1x2 + x2 = 4
<=> (x1 + x2) - 2x1x2=4
<=> 2(m+1) - 2.4 = 4
<=> 2m + 2 - 8 = 4
<=> 2m = 10
<=> m = 5 (T/m)
Đoạn \((\sqrt{x_1}-\sqrt{x_2})^2=4\)
\(\Rightarrow x_1-2\sqrt{x_1x_2}+x_2=4\) chứ bạn.

- xét phương trình hoành độ giao điểm : \(x^2=\left(2m-1\right)x-m+2\)\(\Leftrightarrow x^2-\left(2m-1\right)x+m-2=0\)có \(\Delta=\left(2m-1\right)^2-4\left(m-2\right)=4m^2-8m+9=\left(2m-1\right)^2+8\ge8\)vậy nên phương trinh luôn có 2 nghiệm phân biệt tức hai đồ thị luôn cắt nhau tại 2 điểm phân biệt A và B
- Có viet : \(\hept{\begin{cases}x_1+x_2=2m-1\\x_1x_2=m-2\end{cases}}\)ta có : \(A\left(x_1,y_1\right)=A\left(x_1,x_1^2\right)\)và \(B\left(x_2,y_2\right)=B\left(x_2,x_2^2\right)\)
nên ta có : \(x_1y_1+x_2y_2=0\Leftrightarrow x_1^3+x_2^3=0\)\(\Leftrightarrow\left(x_1+x_2\right)\left(\left(x_1+x_2\right)^2-3x_1x_2\right)=0\)\(\Leftrightarrow\left(2m-1\right)\left[\left(2m-1\right)^2-3m+6\right]=0\)
- \(2m-1=0\Leftrightarrow m=\frac{1}{2}\)
- \(\left(2m-1\right)^2-3m+6=0\Leftrightarrow4m^2-7m-7=0\)VN
2. Cho parabol (P): y = x2 và đường thẳng (d): y = 2(m – 1)x + m2 + 2m (m là tham số, m ∈ R )
a) Chứng minh rằng đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt A, B?
b) Gọi H và K lần lượt là hình chiếu của A và B trên trục hoành.
Tìm m sao cho: OH2 + OK2 = 6 mọi người hướng dẫ mk ý b vs

a: Thay x=-1 và y=3 vào (d), ta được:
-2-m+1=3
=>-1-m=3
=>m+1=-3
hay m=-4