Giải hệ phương trình
56x=4y
x( z - 24 )= (y - x)( 80 - z)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
24 tháng 1 2021
\(\text{⋄}\)Xét xyz = 0 thì dễ có x = y = z = 0 (Nếu giả sử x = 0 thì 4y2(1 - x) = 0 hay y = 0 do đó 4z2(1 - y) = 0 suy ra z = 0, tương tự đối với y, z = 0)
\(\text{⋄}\)Xét \(xyz\ne0\)thì từ hệ suy ra \(xyz=64x^2y^2z^2\left(1-x\right)\left(1-y\right)\left(1-z\right)\Leftrightarrow64xyz\left(1-x\right)\left(1-y\right)\left(1-z\right)=1\)(*)
Dễ có: \(\left(2x-1\right)^2\ge0\Leftrightarrow4x\left(1-x\right)\le1\), tương tự: \(4y\left(1-y\right)\le1;4z\left(1-z\right)\le1\)suy ra \(64xyz\left(1-x\right)\left(1-y\right)\left(1-z\right)\le1\)
Như vậy điều kiện để (*) xảy ra là \(x=y=z=\frac{1}{2}\)
Vậy hệ có 2 nghiệm \(\left(x,y,z\right)\in\left\{\left(0;0;0\right),\left(\frac{1}{2};\frac{1}{2};\frac{1}{2}\right)\right\}\)
M
1
CM
7 tháng 11 2019
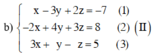
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần ẩn số.
Nhân phương trình (1) với 2 rồi cộng với phương trình (2) và nhân phương trình (1) với (3) rồi trừ đi phương trình (3) ta được:
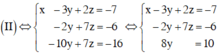
Giải hệ phương trình trên ta được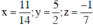 
Vậy hệ phương trình có nghiệm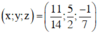 
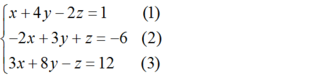
CM
16 tháng 3 2017
Đưa hệ phương trình về dạng hệ tam giác bằng cách khử dần các ẩn.
Nhân phương trình (2) với 2 rồi cộng với phương trình (1) và cộng phương trình (2) với phương trình (3) ta được:
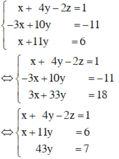
Giải hệ phương trình trên ta được
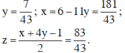
Vậy hệ phương trình có nghiệm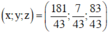 
HP
26 tháng 11 2016
áp dụng bđt \(\frac{a+b}{2}\ge\sqrt{ab}\),dấu "=" xảy ra <=>a=b
\(\sqrt{\left(4x-1\right).1}\le\frac{1+4x-1}{2}=2x\)
Tương tự \(\sqrt{\left(4y-1\right).1}\le\frac{1+4y-1}{2}=2y;\sqrt{\left(4z-1\right).1}\le\frac{1+4z-1}{2}=2z\)
Cộng theo vế:
=>\(2\left(x+y+z\right)\ge\sqrt{4x-1}+\sqrt{4y-1}+\sqrt{4z-1}\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}\sqrt{4x-1}=1\\\sqrt{4y-1}=1\\\sqrt{4z-1}=1\end{cases}}< =>x=y=z=\frac{1}{2}\)
16 tháng 10 2020
| 5xyz=24(x+y)(1) |
| 7xyz=24(y+z)(2) |
xyz=4(x+z) => 2xyz= 8(x+z) (3) Trừ vế theo vế (1),(1),(3) ta được: 7xyz - 5xyz - 2xyz = 24(y+z) - 24(x+y) - 8(x+z) 0 = 16z - 32x => 0 = z - 2x => z=2x Thay z=2x vào (3) ta đươc: 4x^2y = 24x =>xy=6 Thay xy=6; z=2x vào (1) ta được: 5xyz = 24(x+y) <=> 30z= 12z + 24y <=>3z=4y Mà z=2x => 4y=6x <=> 2y=3x Thay 2y=3x vào xy=6 ta được xy=6=> 2xy= 12 <=> 3x^2=12 => x^2=4 => x=(2;-2) +) Với x=2 => y= 3, z= 4 +) Với x=-2 => y= -3, z= -4 Vậy x,y,z= (2,3,4): (-2,-3,-4) |