Một vật được thả rơi tự do từ độ cao 90m so với mặt đất. Lấy g=10m/s2. Hãy tính:
a) Thời gian rơi của vật?
b) Vận tốc lúc chạm đất?
c) Quãng đường vật đi được trong giây cuối cùng?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TK
9 tháng 10 2021
< Nếu thấy mình làm tắt hay làm sai thì comment bên dưới để mình giải thích chỗ đó nha>
a,\(t=\sqrt{\dfrac{2s}{g}}=\sqrt{\dfrac{2\cdot9}{10}}=\dfrac{3}{\sqrt{5}}\left(s\right)\)
b, \(v=gt=10\cdot\dfrac{3}{\sqrt{5}}=6\sqrt{5}\left(\dfrac{m}{s}\right)\)
c, \(s=\dfrac{1}{2}gt^2-\dfrac{1}{2}g\left(t-1\right)^2=\dfrac{1}{2}\cdot10\cdot\left(\dfrac{3}{\sqrt{5}}\right)^2-\dfrac{1}{2}\cdot10\cdot\left(\dfrac{3}{\sqrt{5}}-1\right)^2=-5+6\sqrt{5}\left(m\right)\)
9 tháng 10 2021
a) Thời gian vật rơi: \(S=\dfrac{1}{2}gt^2\Rightarrow t=\sqrt{\dfrac{2S}{g}}=\sqrt{\dfrac{2\cdot9}{10}}=\dfrac{3\sqrt{5}}{5}s\approx1,34s\)
b) Vận tốc lúc chạm đất: \(v=gt=10\cdot\dfrac{3\sqrt{5}}{5}=6\sqrt{5}\) m/s
c) Quãng đường vật đi trong giây cuối:
\(S=\dfrac{1}{2}gt^2-\dfrac{1}{2}g\left(t-1\right)^2=\dfrac{1}{2}\cdot10\cdot\left(\dfrac{3\sqrt{5}}{5}\right)^2-\dfrac{1}{2}\cdot10\cdot\left(\dfrac{3\sqrt{5}}{5}-1\right)^2=6\sqrt{5}-5\approx8,42m\)
10 tháng 10 2021
Đề bài lỗi ạ: Thời gian vật đc thả rơi tự do là 4s.
a) Độ cao của vật so với mặt đất: \(h=\dfrac{1}{2}gt^2=\dfrac{1}{2}\cdot10\cdot4^2=80m\)
b) Vận tốc lúc chạm đất: \(v=gt=10\cdot4=40\)m/s
c) Quãng đường vật đi trong giây cuối:
\(S=\dfrac{1}{2}gt^2-\dfrac{1}{2}g\left(t-1\right)^2=\dfrac{1}{2}\cdot10\cdot4^2-\dfrac{1}{2}\cdot10\cdot\left(4-1\right)^2=35m\)
VT
22 tháng 12 2017
Quãng đường vật rơi trong 1s cuối cùng:
∆ h = h - h 7 = 75 m
VT
31 tháng 8 2019
Đáp án A
Quãng đường vật rơi trong 7s đầu:
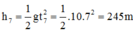
Quãng đường vật rơi trong 1s cuối cùng:
4 tháng 10 2021
a) Độ cao của vật so với đất:
\(S=\dfrac{1}{2}gt^2=\dfrac{1}{2}\cdot10\cdot4^2=80m\)
b) Vận tốc lúc chạm đất:
\(v=gt=10\cdot4=40\)m/s
c) Quãng đường vật đi được trong 4s là 80m.
Quãng đường vật đi được trong 3s là 45m.
Quãng đường vật đi trong giây cuối là S=80-45=35m.
13 tháng 10 2021
a/ \(t=\sqrt{\dfrac{2h}{g}}=6\left(s\right)\)
b/ \(v=\sqrt{2gh}=60\left(m\backslash s^2\right)\)
c/ \(s_{t-1}=\dfrac{1}{2}g\left(t-1\right)^2=125\left(m\right)\)
\(s_{cuoi}=s-s_{t-1}=55\left(m\right)\)
\(\Rightarrow\left\{{}\begin{matrix}a,\Rightarrow t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2.90}{10}}=3\sqrt{2}\left(s\right)\\b,\Rightarrow v=gt=3\sqrt{2}.10=30\sqrt{2}\left(m/s\right)\\c,\Rightarrow\Delta S=h-\dfrac{1}{2}g\left(t-1\right)^2=80-5\left(4-1\right)^2=35m\\\end{matrix}\right.\)