Cho A = 1 + 2 + 22 + 23 + 24 +.....+22008
Chứng minh : A = 22008 - 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = 1 + 2 + 2 2 + . . . + 2 2007
2 A = 2 + 2 2 + . . . + 2 2007 + 2 2008
A = 2A - A = ( 2 + 2 2 + . . . + 2 2007 + 2 2008 ) - ( 1 + 2 + 2 2 + . . . + 2 2007 ) = 2 2008 - 1
Vậy A = 2 2008 - 1

Đặt A=1+2+22+...+220081+2+22+...+22008
=>2A=2.(1+2+22+...+220081+2+22+...+22008)
=>2A=2+22+23+...+220092+22+23+...+22009
=>2A-A=(2+22+23+...+220092+22+23+...+22009)-(1+2+22+...+220081+2+22+...+22008)
=>A=22009−122009−1
=>A=(-1).(−2)2009(−2)2009+(-1).1
=>A=(-1).[(−2)2009+1][(−2)2009+1]
=>A=(-1).(1−22009)(1−22009)
=>1+2+22+...+220081+2+22+...+22008/1-2200922009
=(−1).(1−22009)1−22009(−1).(1−22009)1−22009=-1
Giải:
Đặt A=1+2+22+23+...+22008
2A=2+22+23+24+...+22009
2A-A=(1+2+22+23+...+22008)-(2+22+23+24+...+22009)
A =1-22009
Vậy B=1-22009/1-22009=1
Chúc bạn học tốt!

Ta gọi tử của phân số B là A ta có:
A=1+2+2^2+2^3+...+2^2008
2A=2 + 2^2 + 2^3 + 2^4 +... + 2^2009
=>A=2^2009 - 1
A=-1 + 2^2009
ta thấy tử là số đối của mẫu =>B=\(\dfrac{-1}{1}\)

A=(1+2+2^2)+2^3(1+2+2^2)+...+2^96(1+2+2^2)+2^99
=7(1+2^3+...+2^96)+2^99 ko chia hết cho 7

Lời giải:
$A=(2+2^2)+(2^3+2^4)+....+(2^{99}+2^{100})$
$=2(1+2)+2^3(1+2)+...+2^{99}(1+2)$
$=2.3+2^3.3+...+2^{99}.3$
$=3(2+2^3+...+2^{99})\vdots 3$
Ta có đpcm.

A=\((1+2)+\left(2^2+2^3\right)+...+\left(2^{19}+2^{20}\right)\)
A=\(3.1+2^2\left(1+2\right)+...+2^{19}\left(1+2\right)\)
A=\(3.1+3.2^2+...+3.2^{19}\)
A=\(3\left(1+2^2+...+2^{19}\right)\)\(⋮3\)
Vậy A\(⋮3\)
A=(1+2)+(22+23)+...+(219+220)(1+2)+(22+23)+...+(219+220)
A=3.1+22(1+2)+...+219(1+2)3.1+22(1+2)+...+219(1+2)
A=3.1+3.22+...+3.2193.1+3.22+...+3.219
A=3(1+22+...+219)3(1+22+...+219)⋮3⋮3
NÊN A⋮3

Số số hạng của biểu thức A là: (40-21):1+1=20(số hạng)
Ta có : 1/21>1/40,1/22>1/40,1/23>1/40,...,1/40=1/40
1/21+1/22+1/23+...+1/40>1/40+1/40+1/41+1/40+...+1/40( 20 số 1/40)
A>1/40x20=1/2
A>1/20 (1)
Lại có: 1/21=1/21,1/21>1/22,1/21>1/23,...,1/21>1/40
1/21+1/21+1/21+...+1/21(20 số 1/21)>1/21+1/22+1/23+...+1/40
1/21x20>A
20/21>A.Mà 1>20/21
1>A (2)
Từ (1) và (2) ta có : 1/2<A<1(đpcm)
Vậy bài tôán đđcm
\(\frac{1}{2}=\frac{1}{40}+\frac{1}{40}+....+\frac{1}{40}\)có 20 số hạng \(\)
\(\frac{1}{21}+\frac{1}{22}+....+\frac{1}{40}\)có 20 số hạng
\(\frac{1}{21}>\frac{1}{40}\)
\(\frac{1}{22}>\frac{1}{40}\)
\(.....\)
\(\frac{1}{40}=\frac{1}{40}\)\(\Rightarrow\frac{1}{2}< \frac{1}{21}+\frac{1}{22}+.....+\frac{1}{40}\)
\(1=\frac{1}{40}+....+\frac{1}{40}\)có 40 số hạng mà A chỉ có 20 số hạng
\(\Rightarrow\frac{1}{2}< A< 1\)
Cho A = 1 + 2 + 22 + 23 + 24 +…299 Chứng minh rằng: A chia hết cho 3
Ghi cách làm và đáp án giúp mình

\(A=1+2+2^2+2^3+....+2^{98}+2^{99}\\ \Leftrightarrow A=\left(1+2\right)+\left(2^2+2^3\right)+\left(2^4+2^5\right)+....+\left(2^{98}+2^{99}\right)\\ \Leftrightarrow A=3+2^2.\left(1+2\right)+2^4.\left(1+2\right)+....+2^{98}.\left(1+2\right)\\ \Leftrightarrow A=3+3.2^2+3.2^4+....+3.2^{98}\\ \Leftrightarrow A=3.\left(1+2^2+2^4+...+2^{98}\right)⋮3\)
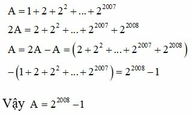
Đề sai à
sửa đề
\(A=1+2+2^2+2^3+2^4+.....+2^{2008}\)
Chứng minh \(A=2^{2009}-1\)
Giải :
\(A=1+2+2^2+2^3+.....+2^{2008}\)
\(2A=2+2^2+2^3+...+2^{2009}\)
\(2A-A=2^{2009}-1\)
\(\Rightarrow A=2^{2009}-1\left(dpcm\right)\)
Study well
uk
đề sai ^^
Cho A = 1 + 2 + 22 + 23 + 24 +.....+22007
Chứng minh : A = 22008 - 1
bn sửa đề gần đúng =))))
thôi thì mơn nhoa