Tìm n thuộc N để n^2+4n là số CP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
0
VA
0
NH
3
23 tháng 6 2021
`a in ZZ`
`=>6n-4 vdots 2n+1`
`=>3(2n+1)-7 vdots 2n+1`
`=>7 vdots 2n+1`
`=>2n+1 in Ư(7)={+-1,+-7}`
`=>2n in {0,-2,6,-8}`
`=>n in {0,-1,3,-4}`
`b in ZZ`
`=>3n+2 vdots 4n-4`
`=>12n+8 vdots 4n-4`
`=>3(4n-4)+20 vdots 4n-4`
`=>20 vdots 4n-4`
`=>4n-4 in Ư(20)={+-1,+-2,+-4,+-5,+-10,+-20}`
`=>4n-4 in {+-4,+-20}`
`=>n-1 in {+-1,+-5}`
`=>n in {0,2,6,-4}`
`c in ZZ`
`=>4n-1 vdots 3-2n`
`=>2(3-2n)-7 vdots 3-2n`
`=>7 vdots 3-2n`
`=>3-2n in Ư(7)={+-1,+-7}`
`=>2n in {4,0,-4,10}`
`=>n in {2,0,-2,5}`
23 tháng 6 2021
a) đk: \(n\ne\dfrac{-1}{2}\)
Để \(\dfrac{6n-4}{2n+1}\) nguyên
<=> \(\dfrac{3\left(2n+1\right)-7}{2n+1}\) nguyên
<=> \(3-\dfrac{7}{2n+1}\) nguyên
<=> \(7⋮2n+1\)
Ta có bảng
| 2n+1 | 1 | -1 | 7 | -7 |
| n | 0 | -1 | 3 | -4 |
| tm | tm | tm | tm |
b)đk: \(n\ne1\)
Để \(\dfrac{3n+2}{4n-4}\) nguyên
=> \(\dfrac{3n+2}{n-1}\) nguyên
<=> \(\dfrac{3\left(n-1\right)+5}{n-1}\) nguyên
<=> \(3+\dfrac{5}{n-1}\) nguyên
<=> \(5⋮n-1\)
Ta có bảng:
| n-1 | 1 | -1 | 5 | -5 |
| n | 2 | 0 | 6 | -4 |
| Thử lại | tm | loại | tm | loại |
c) đk: \(n\ne\dfrac{3}{2}\)
Để \(\dfrac{4n-1}{3-2n}\) nguyên
<=> \(\dfrac{4n-1}{2n-3}\) nguyên
<=> \(\dfrac{2\left(2n-3\right)+5}{2n-3}\) nguyên
<=> \(2+\dfrac{5}{2n-3}\) nguyên
<=> \(5⋮2n-3\)
Ta có bảng:
| 2n-3 | 1 | -1 | 5 | -5 |
| n | 2 | 1 | 4 | -1 |
| tm | tm | tm | tm |
22 tháng 7 2023
\(\dfrac{4n^2-9}{2n+3}=\dfrac{\left(2n+3\right)\left(2n-3\right)}{2n+3}=2n-3\)
Để \(\dfrac{4n^2-9}{2n+3}\) là số nguyên
\(\Rightarrow2n-3\in Z\)
\(\Rightarrow\forall n\in Z\)
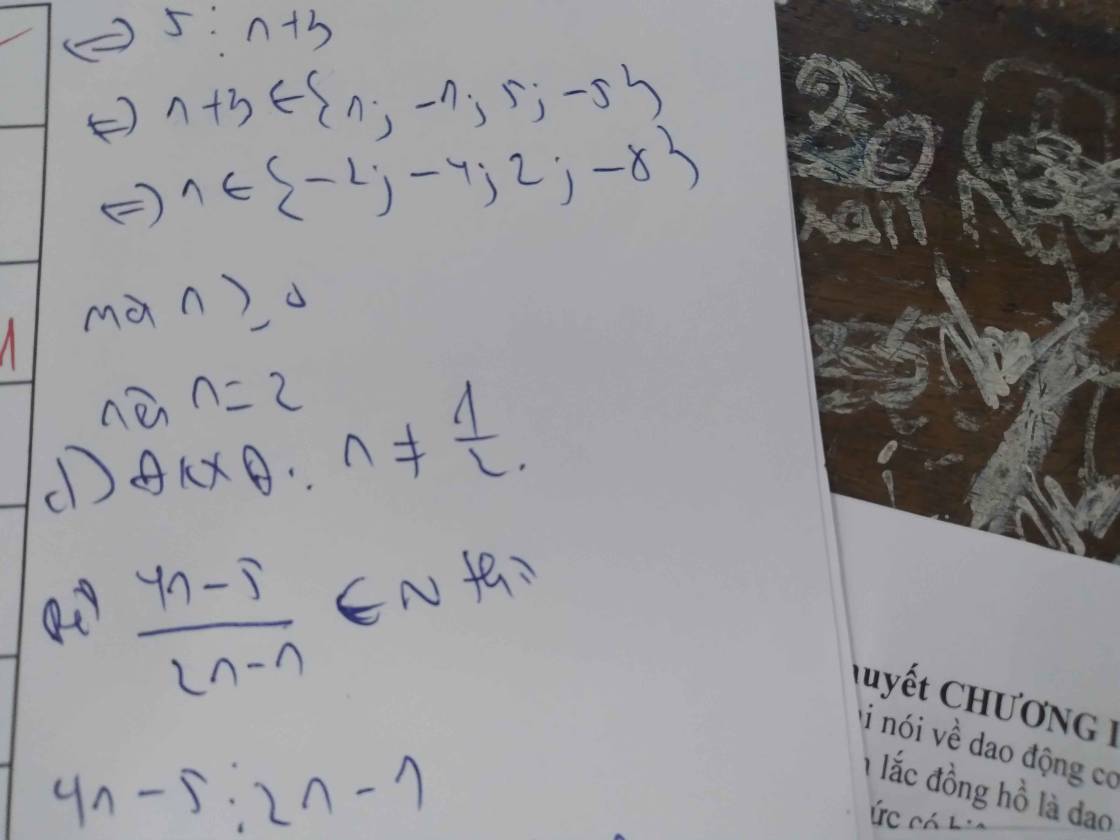
Ta co:\(n^2+4n=k^2\)
\(\Leftrightarrow\left(n+2\right)^2-4=k^2\)
\(\Leftrightarrow\left(n+2\right)^2-k^2=4\)
\(\Leftrightarrow\left(n+k+2\right)\left(n-k+2\right)=4\)
Ma \(4=4.1=2.2\)
Suy ra:
\(\hept{\begin{cases}n+k+2=1\\n-k+2=4\end{cases}\left(1\right)}\)
\(\hept{\begin{cases}n+k+2=2\\n-k+2=2\end{cases}\left(2\right)}\)
Xet (1) ta duoc:
\(\hept{\begin{cases}n=1\\k=-2\end{cases}}\)
Thay vao thay khong thoa man nen loai
Xet (2) ta duoc:
\(\hept{\begin{cases}n=0\\k=0\end{cases}}\)
Thay vao thay thoa man nen nhan
Vay \(n=0\)thi \(n^2+4n\)la so chinh phuong
Với n = 0 thì nó là số chính phương (chọn)
Với n > 0 thì ta có\(n^2< n^2+4n< \left(n+2\right)^2\)
\(\Rightarrow n^2+4n=\left(n+1\right)^2\)
\(\Leftrightarrow4n=2n+1\Leftrightarrow n=\frac{1}{2}\left(KTM\right)\)
Vậy n = 0
P/s: Lâu ko làm dạng này nên ko chắc nha!