đề bài hai điểm AvàB thuộc cùng một nửa mặt phawrg có bờ là đường thẳng xy.Khoảng cách từ A đến xy bằng 12cm,khoảng cách từ điểm B đến xy bằng 20cm.Tính khoảng cách tứ trung điểm C của AB đến xy. Làm ơn giải giùm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 3 2017
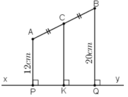
Gọi P, Q, K lần lượt là chân đường vuông góc hạ từ A, B, C xuống xy.
+ AP ⊥ xy và BQ ⊥ xy ⇒ AP // BQ
⇒ Tứ giác ABQP là hình thang.
+ CK ⊥ xy ⇒ CK // AP//BQ
+ Hình thang ABQP có AC = CB (gt) và CK // AP // BQ
⇒ PK = KQ
⇒ CK là đường trung bình của hình thang
⇒ CK = (AP + BQ)/2.
Mà AP = 12cm, BQ = 20cm ⇒ CK = 16cm.
Vậy khoảng cách từ trung điểm C của AB đến xy bằng 16cm.
20 tháng 9 2016
Kẻ AH, CM, BK vuông góc với xy (H, M, K là chân đường vuông góc).
Hình thang ABKH có AC = CB,
CM // AH // BK
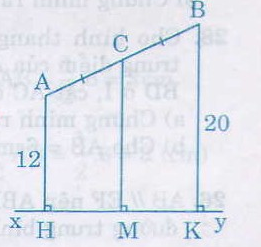
nên MH = MK và CM là đường trung bình.
Do đó CM = = 16 (cm)
HH
8 tháng 7 2020
Gọi P, Q, K lần lượt là chân đường vuông góc hạ từ A, B, C xuống xy.
+ AP ⊥ xy và BQ ⊥ xy => AP // BQ
=> Tứ giác ABQP là hình thang.
+ CK ⊥ xy => CK // AP// BQ
+ Hình thang ABQP có AC = CB ( gt ) và CK // AP // BQ
=> PK = KQ
=> CK là đường trung bình của hình thang
=> CK = (AP + BQ)/2
Mà AP = 12cm, BQ = 20cm => CK = 16cm.
Vậy khoảng cách từ trung điểm C của AB đến xy bằng 16cm .
G
16 tháng 9 2014
AH, CM, BK vuông góc với xy nên 3 đường thẳng đó song song với nhau
=> AHKB là hình thang và CM là đường trung bình của hình thang
=> CM = 1/2 (AH + BK) = 1/2 (12 + 20) = 16 cm
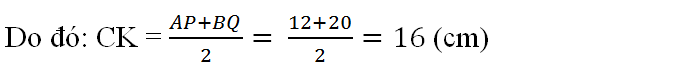
Kẻ AP, CK, BQ vuông góc với xy (P, K, Q là chân đường vuông góc).
Hình thang APQB có : \(\hept{\begin{cases}AC=CB\\CK//AP//BQ\end{cases}}\)
=> KP = KQ (hình chiếu của hai đoạn thẳng bằng nhau)
=> CK là đường trung bình và cũng là khoảng cách từ trung điểm C của AB đến xy.
Do đó : \(CK=\frac{AP+BQ}{2}=\frac{12+20}{2}=6\left(cm\right)\)
Vậy khoảng cách từ trung điểm C của AB đến xy là CK=16(cm) .
Chúc bạn học tốt !!!
thank bạn nha