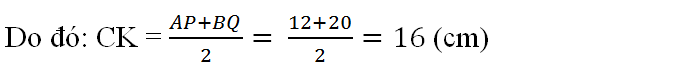Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A C B P K Q x y
Kẻ AP, CK, BQ vuông góc với xy (P, K, Q là chân đường vuông góc).
Hình thang APQB có : \(\hept{\begin{cases}AC=CB\\CK//AP//BQ\end{cases}}\)
=> KP = KQ (hình chiếu của hai đoạn thẳng bằng nhau)
=> CK là đường trung bình và cũng là khoảng cách từ trung điểm C của AB đến xy.
Do đó : \(CK=\frac{AP+BQ}{2}=\frac{12+20}{2}=6\left(cm\right)\)
Vậy khoảng cách từ trung điểm C của AB đến xy là CK=16(cm) .
Chúc bạn học tốt !!!

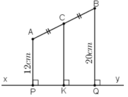
Gọi P, Q, K lần lượt là chân đường vuông góc hạ từ A, B, C xuống xy.
+ AP ⊥ xy và BQ ⊥ xy ⇒ AP // BQ
⇒ Tứ giác ABQP là hình thang.
+ CK ⊥ xy ⇒ CK // AP//BQ
+ Hình thang ABQP có AC = CB (gt) và CK // AP // BQ
⇒ PK = KQ
⇒ CK là đường trung bình của hình thang
⇒ CK = (AP + BQ)/2.
Mà AP = 12cm, BQ = 20cm ⇒ CK = 16cm.
Vậy khoảng cách từ trung điểm C của AB đến xy bằng 16cm.

Kẻ AH, CM, BK vuông góc với xy (H, M, K là chân đường vuông góc).
Hình thang ABKH có AC = CB,
CM // AH // BK
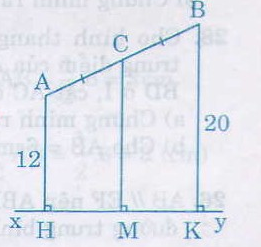
nên MH = MK và CM là đường trung bình.
Do đó CM = = 16 (cm)

A C B P K Q x Y 12 20
Gọi P, Q, K lần lượt là chân đường vuông góc hạ từ A, B, C xuống xy.
+ AP ⊥ xy và BQ ⊥ xy => AP // BQ
=> Tứ giác ABQP là hình thang.
+ CK ⊥ xy => CK // AP// BQ
+ Hình thang ABQP có AC = CB ( gt ) và CK // AP // BQ
=> PK = KQ
=> CK là đường trung bình của hình thang
=> CK = (AP + BQ)/2
Mà AP = 12cm, BQ = 20cm => CK = 16cm.
Vậy khoảng cách từ trung điểm C của AB đến xy bằng 16cm .

A B C H K M x y 12 20
AH, CM, BK vuông góc với xy nên 3 đường thẳng đó song song với nhau
=> AHKB là hình thang và CM là đường trung bình của hình thang
=> CM = 1/2 (AH + BK) = 1/2 (12 + 20) = 16 cm