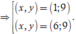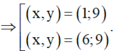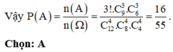. Có 10 học sinh thi học sinh giỏi chia làm 2 nhóm, nhóm I có 6 học sinh, nhóm II có 4 học sinh. Xác suất để một học sinh trong mỗi nhóm đạt giải tương ứng lần lượt là 0,8 và 0,7.
a) Phỏng vấn ngẫu nhiên 2 học sinh, tính xác suất cả 2 em đều ở nhóm I.
b) Tính xác suất để một học sinh bất kì đạt giải