Tìm GTNN của x4 - 7x2 + 4x + 25
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đa thức đã cho là bậc 3 theo biến x khi và chỉ khi:
\(\left\{{}\begin{matrix}m^2-25=0\\20+4m\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m=\pm5\\m\ne-5\end{matrix}\right.\)
\(\Rightarrow m=5\)

Giải phương trình??? sử dụng Hooc-ne cho nhanh nhá :v
1) \(x^4-8x^2+4x+3=0\)
( dùng máy tính ta đoán được 1 nghiệm chính xác là -3 )
\(\Leftrightarrow\left(x+3\right)\left(x^3-3x^2+x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x^3-3x^2+x+1=0\left(2\right)\end{matrix}\right.\)
Tiếp tục dùng máy tính ta tìm được 1 nghiệm chính xác của pt ( 2 ) là 1
\(\Leftrightarrow\left(x+3\right)\left(x-1\right)\left(x^2-2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-1=0\\x^2-2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\\x=1+\sqrt{2}\\x=1-\sqrt{2}\end{matrix}\right.\)
rồi mấy câu còn lại tương tự

Lời giải:
$A=x^4-4x^3+7x^2-12x+75$
$=(x^2-2x)^2+3x^2-12x+75$
$=(x^2-2x)^2+3(x^2-4x+4)+63$
$=(x^2-2x)^2+3(x-2)^2+63\geq 63$
Vậy $A_{\min}=63$. Giá trị này đạt tại $x^2-2x=x-2=0$
$\Leftrightarrow x=2$

\(A=\left(x^4-4x^3+4x^2\right)+\left(3x^2-12x+12\right)+63\)
\(A=x^2\left(x^2-4x+4\right)+3\left(x^2-4x+4\right)+63\)
\(A=\left(x^2+3\right)\left(x-2\right)^2+63\ge63\)
\(A_{min}=63\) khi \(x=2\)

1: A=(x-1)^2>=0
Dấu = xảy ra khi x=1
5: B=-(x^2+6x+10)
=-(x^2+6x+9+1)
=-(x+3)^2-1<=-1
Dấu = xảy ra khi x=-3
2: B=x^2+4x+4-9
=(x+2)^2-9>=-9
Dấu = xảy ra khi x=-2
6: =-(x^2-5x-3)
=-(x^2-5x+25/4-37/4)
=-(x-5/2)^2+37/4<=37/4
Dấu = xảy ra khi x=5/2
3: =x^2+x+1/4-1/4
=(x+1/2)^2-1/4>=-1/4
Dấu = xảy ra khi x=-1/2
7: =4x^2+4x+1-2
=(2x+1)^2-2>=-2
Dấu = xảy ra khi x=-1/2

Sửa đề:
\(E=x^4-2x^3+3x^2-4x+2022\)
\(=\left(x^4-2x^3+x^2\right)+\left(2x^2-4x+2\right)+2020\)
\(=\left(x^2-x\right)^2+2\left(x-1\right)^2+2020\)
Vì \(\left(x^2-x\right)^2+2\left(x-1\right)^2\ge0\forall x\)
\(\Rightarrow E\ge2020\)
\(MinE=2020\Leftrightarrow\left\{{}\begin{matrix}x^2-x=0\\x-1=0\end{matrix}\right.\)\(\Leftrightarrow x=1\)

1. x2-8x+1 = x2 -2x.4 + 42 - 42 +1 = ( x- 4 )2 - 15
mà ( x - 4 )2 > 0
=> ( x - 4 )2 -15 > 0
Vậy -15 là gt min của biểu thức khi x = 4
2. x2 - 4x + y2 - 6y + 2 = x2 - 2.2x + 22 + y2 - 2.3y + 32 -11 = (x-2)2 + ( y - 3)2 -11
mà ( x - 2)2 > 0
( y - 3)2 > 0
Vậy -11 là gt min của biểu thức khi x=2 và y = 3
Mình nghĩ là bài 3 là tìm gt lớn nhất chứ bạn ^^

a: Ta có: \(\left(2x-3\right)^2+6\left(2x-1\right)=7\)
\(\Leftrightarrow\left(2x-3\right)^2+6\left(2x-1\right)-7=0\)
\(\Leftrightarrow4x^2-12x+9+12x-6-7=0\)
\(\Leftrightarrow4x^2=4\)
\(\Leftrightarrow x^2=1\)
hay \(x\in\left\{1;-1\right\}\)
b: Ta có: \(x^2-7x+10=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=2\end{matrix}\right.\)

a) \(\left(2x-3\right)^2+6\left(2x-1\right)=7\\ \Rightarrow4x^2-12x+9+12x-6-7=0\\ \Rightarrow4x^2-4=0\\ \Rightarrow x^2-1=0\\ \Rightarrow x^2=1\\ \Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
b) \(x^2-7x+10=0\\ \Rightarrow\left(x^2-2x\right)-\left(5x-10\right)=0\\ \Rightarrow\left(x-2\right)\left(x-5\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-2=0\\x-5=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)
c) \(-6x^2+13x-5=0\\ \Rightarrow-\left(6x^2-13x+5\right)=0\\ \Rightarrow-\left[\left(6x^2-10x\right)-\left(3x-5\right)\right]=0\\ \Rightarrow-\left[2x\left(3x-5\right)-\left(3x-5\right)\right]=0\\ \Rightarrow-\left(2x-1\right)\left(3x-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}-\left(2x-1\right)=0\\3x-5=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}2x-1=0\\3x-5=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{5}{3}\end{matrix}\right.\)
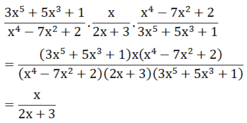
\(x^4-7x^2+4x+25\)
\(=x^4-8x^2+16+x^2+4x+4+5\)
\(=\left(x^2-4\right)^2+\left(x+2\right)^2+5\ge5\forall x\)
Dấu"=" xảy ra<=> \(\hept{\begin{cases}\left(x^2-4\right)^2=0\\\left(x+2\right)^2=0\end{cases}\Rightarrow\hept{\begin{cases}x^2=4\\x=-2\end{cases}\Rightarrow}x=-2}\)
Vậy GTNN của bt = 5 tại x=-2