tìm gtnn của biểu thức sau;k=x^2+5y^2+2xy-2x+2015
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 9 2021
\(-\left|2-3x\right|\le0\forall x\)
\(\Leftrightarrow-\left|3x-2\right|+\dfrac{1}{2}\le\dfrac{1}{2}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{2}{3}\)
18 tháng 10 2021
a) \(A=4x^2-4x+9=\left(4x^2-4x+1\right)+8\)
\(=\left(2x-1\right)^2+8\ge8\)
\(minA=8\Leftrightarrow x=\dfrac{1}{2}\)
c) \(C=\left(x^2-4x+4\right)+\left(y^2+5y+\dfrac{25}{4}\right)-\dfrac{13}{4}\)
\(=\left(x-2\right)^2+\left(y+\dfrac{5}{2}\right)^2-\dfrac{13}{4}\ge-\dfrac{13}{4}\)
\(minC=-\dfrac{13}{4}\Leftrightarrow\) \(\left\{{}\begin{matrix}x=2\\y=-\dfrac{5}{2}\end{matrix}\right.\)
21 tháng 4 2021
1. B = | x - 2018 | + | x - 2019 | + | x - 2020 |
= ( | x - 2018 | + | x - 2020 | ) + | x - 2019 |
= ( | x - 2018 | + | 2020 - x | ) + | x - 2019 |
Vì \(\hept{\begin{cases}\left|x-2018\right|+\left|2020-x\right|\ge\left|x-2018+2020-x\right|=2\\\left|x-2019\right|\ge0\end{cases}}\)=> B ≥ 2 ∀ x
Dấu "=" xảy ra <=> \(\hept{\begin{cases}\left(x-2018\right)\left(2020-x\right)\ge0\\x-2019=0\end{cases}}\Rightarrow x=2019\)
Vậy MinB = 2 <=> x = 2019
21 tháng 4 2021
2. ĐKXĐ : x ≥ 0
Ta có : \(\sqrt{x}+3\ge3\forall x\ge0\)
=> \(\frac{2019}{\sqrt{x}+3}\le673\forall x\ge0\). Dấu "=" xảy ra <=> x = 0 (tm)
Vậy MaxC = 673 <=> x = 0
28 tháng 11 2021
Ta thấy:
IX+2/3I luôn lớn hoặc bằng 0
=>IX+2/3I+2 luôn lớn hơn hoặc bằng 2
=>Để M lớn nhất thì M phải bằng 2
Vậy GTNN của M là 2
DX
28 tháng 11 2021
Ta có \(\left|x+\dfrac{2}{3}\right|\ge0\) với mọi x
\(\Rightarrow\left|x+\dfrac{2}{3}\right|+2\ge2\) với mọi x
\(\Rightarrow M\ge2\) với mọi x
Dấu bằng xảy ra khi và chỉ khi \(\left|x+\dfrac{2}{3}\right|=0\)
\(\Leftrightarrow x+\dfrac{2}{3}=0\)
\(\Leftrightarrow x=-\dfrac{2}{3}\)
Vậy Mmin = 2 \(\Leftrightarrow x=-\dfrac{2}{3}\)
12 tháng 10 2021
\(A=\dfrac{b^2}{b-1}=\dfrac{b^2-1+1}{b-1}=b+1+\dfrac{1}{b-1}=b-1+\dfrac{1}{b-1}+2\)
Áp dụng BĐT cosi cho \(b>0\left(b>1\right)\)
\(A=b-1+\dfrac{1}{b-1}+2\ge2\sqrt{\left(b-1\right)\cdot\dfrac{1}{b-1}}+2=2+2=4\)
Dấu \("="\Leftrightarrow\left(b-1\right)^2=1\Leftrightarrow\left[{}\begin{matrix}b-1=1\\b-1=-1\left(ktm\right)\end{matrix}\right.\Leftrightarrow b=2\left(tm\right)\)
NP
2
HP
13 tháng 5 2016
A=x2+5x+8
A=\(x^2+5x+\frac{25}{4}+\frac{7}{4}\)
\(A=x^2+\frac{5}{2}x+\frac{5}{2}x+\frac{25}{4}+\frac{7}{4}\)
\(A=x\left(x+\frac{5}{2}\right)+\frac{5}{2}\left(x+\frac{5}{2}\right)+\frac{7}{4}\)
\(A=\left(x+\frac{5}{2}\right)\left(x+\frac{5}{2}\right)+\frac{7}{4}=\left(x+\frac{5}{2}\right)^2+\frac{7}{4}\)
Vì \(\left(x+\frac{5}{2}\right)^2\ge0\Rightarrow\left(x+\frac{5}{2}\right)^2+\frac{7}{4}\ge\frac{7}{4}\)
=>GTNN của A là 7/4
Dấu "=" xảy ra <=> \(\left(x+\frac{5}{2}\right)^2=0\Leftrightarrow x=-\frac{5}{2}\)
12 tháng 9 2021
\(A=x^2+y^2-8x-y+68=\left(x-4\right)^2+\left(y-\dfrac{1}{2}\right)^2+\dfrac{207}{4}\ge\dfrac{207}{4}\)
\(minA=\dfrac{207}{4}\Leftrightarrow\)\(\left\{{}\begin{matrix}x=4\\y=\dfrac{1}{2}\end{matrix}\right.\)
12 tháng 9 2021
\(A=x^2-8x+y^2-y+68\)
\(=x^2-8x+16+y^2-y+\dfrac{1}{4}+\dfrac{207}{4}\)
\(=\left(x-4\right)^2+\left(y-\dfrac{1}{2}\right)^2+\dfrac{207}{4}\ge\dfrac{207}{4}\forall x,y\)
Dấu '=' xảy ra khi x=4 và \(y=\dfrac{1}{2}\)
30 tháng 7 2023
\(\sqrt{x}-2>=-2\)
=>\(P=\dfrac{5}{\sqrt{x}-2}< =-\dfrac{5}{2}\)
Dấu = xảy ra khi x=0
Vậy: Giá trị lớn nhất của P là -5/2 khi x=0
KR
7 tháng 5 2018
Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự
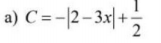
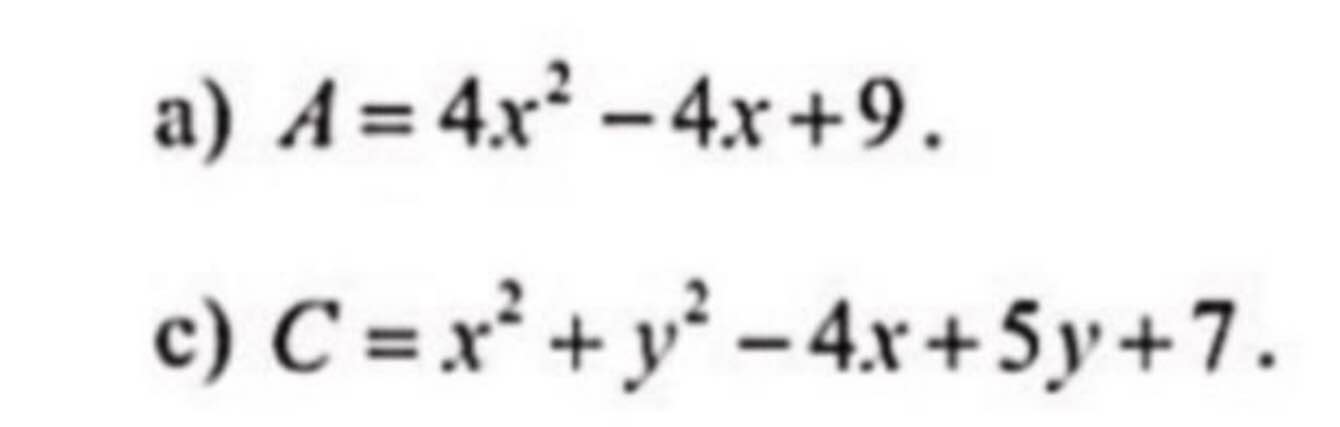
\(k=x^2+2xy+y^2-2x-2y+1+2y+4y^2+2014=\left(x+y-1\right)^2+\left(2y+\frac{1}{2}\right)^2+2013,75\ge0+0+2013,75=2013,75\Rightarrow k_{min}=2013,75\Leftrightarrow\left\{{}\begin{matrix}x+y=1\\y=\frac{-1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\frac{5}{4}\\y=\frac{-1}{4}\end{matrix}\right.\)