Chứng minh rằng : nếu ABCD là tứ giác nội tiếp thì AB. CD + AD. BC = AC. BD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BB
bé Bắp
14 tháng 8 2019
Đúng(0)
TM
Tiểu mực mực
13 tháng 8 2019
https://i.imgur.com/WBXskL5.jpg
Đúng(0)
Những câu hỏi liên quan
23 tháng 5 2015
+) Dễ có tam giác OAB đồng dạng với tam giác ODC (góc AOB = DOC do đối đỉnh; góc BAC = BDC do góc nội tiếp cùng chắn cung BC)
=> \(\frac{OA}{OD}=\frac{OB}{OC}=\frac{AB}{DC}=\frac{a}{c}\)
+) Tương tự, tam giác OAD đồng dạng với tam giác OBC (g - g)
=> \(\frac{OA}{OB}=\frac{OD}{OC}=\frac{AD}{BC}=\frac{b}{d}\)
+) Ta có: \(\frac{OB}{OC}+\frac{OD}{OC}=\frac{a}{c}+\frac{b}{d}=\frac{ad+bc}{cd}\)=> \(\frac{OB+OD}{OC}=\frac{BD}{OC}=\frac{ad+bc}{cd}\Rightarrow\frac{OC}{BD}=\frac{cd}{ad+bc}\) (1)
+) ta có: \(\frac{OA}{OD}=\frac{a}{c};\frac{OA}{OB}=\frac{b}{d}\Rightarrow\frac{OD}{OA}=\frac{c}{a};\frac{OB}{OA}=\frac{d}{b}\)
=> \(\frac{OD}{OA}+\frac{OB}{OA}=\frac{BD}{OA}=\frac{c}{a}+\frac{d}{b}=\frac{bc+ad}{ab}\Rightarrow\frac{OA}{BD}=\frac{ab}{bc+ad}\)(2)
Từ (1)(2) => \(\frac{OC}{BD}+\frac{OA}{BD}=\frac{cd+ab}{ad+bc}\Rightarrow\frac{AC}{BD}=\frac{ab+cd}{ad+bc}\)
PT
1
CM
16 tháng 8 2019
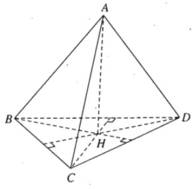
Vẽ AH ⊥ (BCD) tại H, ta có CD ⊥ AH và vì CD ⊥ AB ta suy ra CD ⊥ BH. Tương tự vì BD ⊥ AC ta suy ra BD ⊥ CH
Vậy H là trực tâm của tam giác BCD tức là DH ⊥ BC
Vì AH ⊥ BC nên ta suy ra BC ⊥ AD
Cách khác: Trước hết ta hãy chứng minh hệ thức:
với bốn điểm A, B, C, D bất kì.
Thực vậy , ta có:
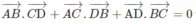
Do đó nếu AB ⊥ CD nghĩa là
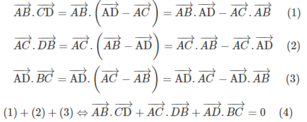
Từ hệ thức (4) ta suy ra
,
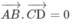do đó AD ⊥ BC.
17 tháng 3 2019
Gọi đường tròn (BIC) cắt BD trại G khác B. Trên đoạn AD lấy E' sao cho AE' = AF.
Xét \(\Delta\)AIF và \(\Delta\)AIE': AF = AE', ^IAF = ^IAE', AI chung => \(\Delta\)AIF = \(\Delta\)AIE' (c.g.c) => IF = IE'
Xét (BIC): ^FBG nội tiếp, BI là phân giác ^FBG, I thuộc (BIC) => (IF = (IG => IF = IG. Từ đó IG = IE'
Dễ thấy: ^IE'A = ^IFA (Do \(\Delta\)AIF = \(\Delta\)AIE') => ^IFB = ^IE'D hay ^IE'D = ^IGD
Từ đó: ^GID = ^E'ID (Vì ^IDE' = ^IDG), kết hợp với IG = IE', cạnh ID chung => \(\Delta\)DGI = \(\Delta\)DE'I (c.g.c)
Suy ra: DG = DE'. Ta lại có: ^CAB = ^CDB; ^CFB = ^CGB => ^FCA = ^GCD
Xét \(\Delta\)CFA và \(\Delta\)CGD: CA = CD; ^CAF = ^CDG; ^FCA = ^GCD => \(\Delta\)CFA = \(\Delta\)CGD (g.c.g)
=> AF = DG. Mà DG = DE' nên AF = DE'. Do đó: DE' = AE' => E' là trung điểm AD => E' trùng E
Như vậy AE = AF và IF = IE suy ra AI là trung trực của EF hay AI vuông góc EF (đpcm),
CM
7 tháng 12 2017
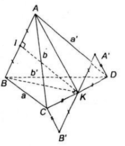
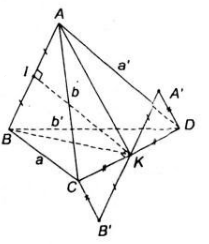
Gọi I, K lần lượt là trung điểm của cạnh AB và CD
Qua K kẻ đường thẳng d // AB, trên d lấy A', B' sao cho K là trung điểm của A'B' và
KA' = IA
* Xét tam giác CKB’ và DKA’ có:
KC= KD ( giả thiết)
KB’= KA’( cách dựng)
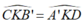( hai góc đối đỉnh )
=> ∆ CKB’ = ∆ DKA’ ( c.g.c)
=> B’C = A’D
*Xét tứ giác IBB’K có IB= KB’ và IB // KB’ ( cách dựng)
=> Tứ giác IBB’K là hình bình hành
=> BB’ // IK (1)
Chứng minh tương tự, ta có: AA’// IK (2)
Từ (1) và (2) suy ra: BB’// IK// AA’ (*)
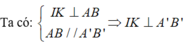
Lại có:IK ⊥ CK
=> IK ⊥ (CKB') (**)
Từ (*) và (**) suy ra BB' ⊥ (CKB') ; AA' ⊥ (CKB')
⇒ BB' ⊥ B'C; AA' ⊥ A'D
* Xét hai tam giác vuông BCB’ và ADA’ có:
BB’ = AA’ (= IK)
CB’ = A’D (chứng minh trên)
=> ∆ BCB’ = ∆ ADA’ ( cạnh huyền –cạnh góc vuông)
=> BC= AD.
* Chứng minh tương tự, AC = BD
