Cho ( d1 ) y = -mx - 2m + 3. ; ( d2 ) x - my - 2 + m
CMR : giao điểm của 2 đoạn thẳng trên di chuyển trên một đường tròn cố định khi m thay đổi , xác định tâm đường tròn đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để hai đường thẳng vuông góc thì m(2m-3)=-1
\(\Leftrightarrow\left(m-1\right)\left(2m-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\\m=\dfrac{1}{2}\end{matrix}\right.\)


b) d 1 cắt trục hoành tại điểm có hoành độ bằng – 3 khi:
0 = -3m + 2m - 1 ⇔ -m - 1 = 0 ⇔ m = -1
Vậy với m = -1 thì d 1 cắt trục hoành tại điểm có hoành độ bằng – 3


a. Gọi A là điểm 3 đường thẳng đồng quy
Phương trình hoành độ giao điểm của d1 và d2: 4/3x + 1= x-1 ⇔ 1/3x = -2 ⇔ x = -6
thay x = -6 vào d2 ⇒ y = -6 -1 = -7
Vậy A(-6;-7)
Để 3 đường thẳng đồng quy thì A thuộc d3 ⇒ -7 = m.(-6) + m+ 3
⇔ -7 = -6m + m + 3
⇔ -5m = -10
⇔ m=2
câu b
a. Gọi A là điểm 3 đường thẳng đồng quy
Phương trình hoành độ giao điểm của d1 và d2: x - m + 1= 2x ⇔ x = -m +1
thay x = -m +1 vào d2 ⇒ y = 2.(-m +1) = -2m +2
Vậy A(-m +1;-2m +2)
Để 3 đường thẳng đồng quy thì A thuộc d3 ⇒ -2m +2 = 2(2m-1).(-m +1) + 1/4
⇔ -2m +2 = -4m² +4m +2m-2 + 1/4
⇔ 4m² - 8m +15m/4=0
Giai pt bậc 2 được m=5/4 và m=3/4

c) Giả sử đường thẳng d 1 luôn đi qua một điểm cố định ( x 1 ; y 1 ) với mọi giá trị của m.
⇒ y 1 = m x 1 + 2m - 1 với mọi m
⇔ m( x 1 + 2) - 1 - y 1 = 0 với mọi m
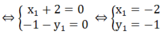
Vậy điểm cố định mà d 1 luôn đi qua với mọi giá trị của m là (-2; -1).

Điều kiện để (d1) và (d2) trùng nhau là
\(\begin{cases}m=2m-3\left(1\right)\\-2m-4=m^2-1\left(2\right)\end{cases}\)
Giải (1) được m = -3
Giải (2) được \(m^2+2m+3=0\) vô nghiệm.
Vậy ........................................