Question

[Trần Ngọc Thảo]

Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O) . Từ A vẽ hai tiếp tuyến AB , AC của đường tròn (O) ( B và C là hai tiếp điểm ) . Gọi H là giao điểm của OA và BC

1) Chứng minh OA ⊥ BC tại H

2) Từ B vẽ đường kính BD của đường trong (O) , đường thẳng AD cắt (O) tại E (khác D) . Chứng minh AE.AD = AH.AO

3) Qua (O) vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F . Chứng minh FD là tiếp tuyến của đường tròn (O)

Các bạn sử dụng kiến thức của hình chương 2 đường tròn để giải cho mk câu 2 và 3 nha . Mk đang cần rất gấp bạn nào giải đúng mk tick cho

Answer 1

[Dinh Thi Hai Ha]

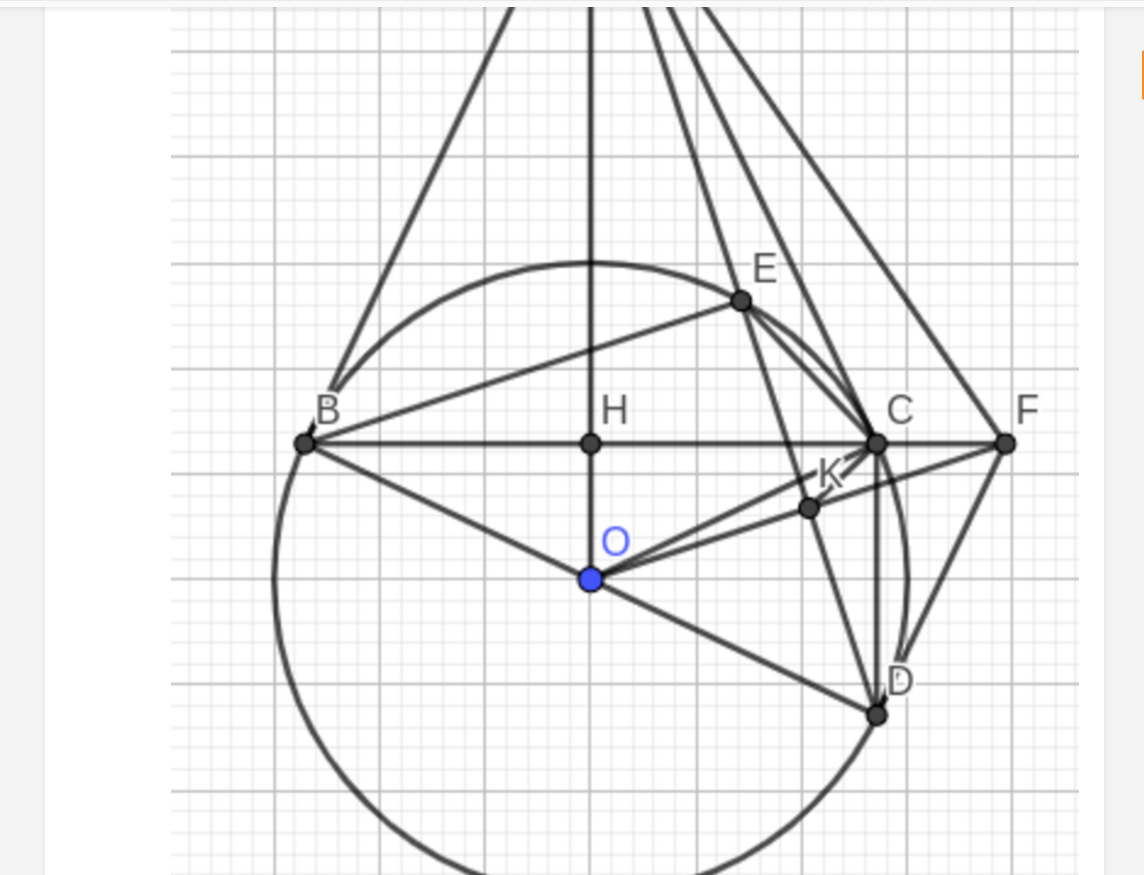
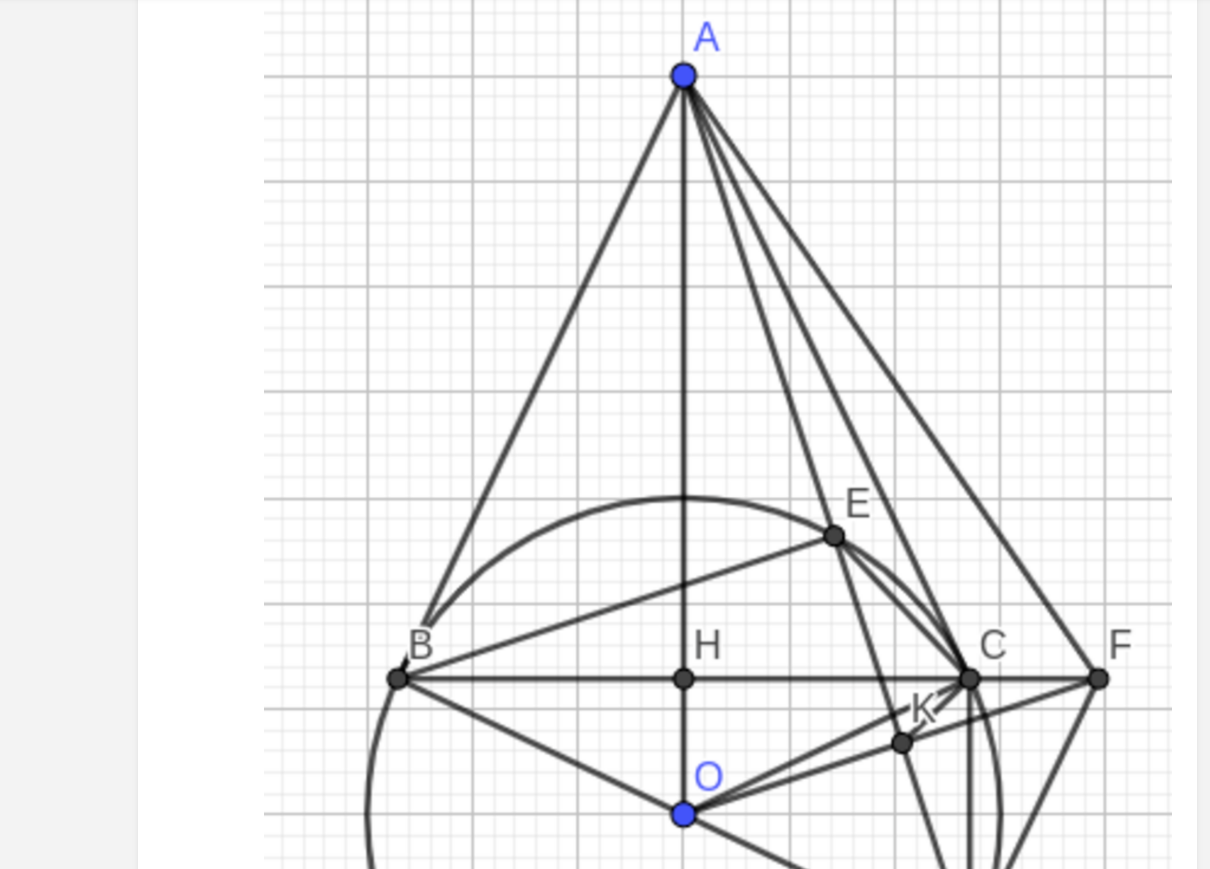
Hình bạn tự vẽ nhé.

a) Xét \(\Delta ABH\) và \(\Delta ACH\) có:

AB=AC ( AB,AC là tiếp tuyến )

\(\widehat{BAH}=\widehat{CAH}\) ( AB,AC là tiếp tuyến )

AH là cạnh chung

\(\Rightarrow\Delta ABH=\Delta ACH\left(c-g-c\right)\)

\(\widehat{\Rightarrow BHA}=\widehat{CHA}\)( hai góc tương ứng )

Ta có : \(\widehat{BHA}+\widehat{CHA}=180^0\) ( hai góc kề bù )

mà \(\widehat{BHA}=\widehat{CHA}\left(cmt\right)\)

\(\Rightarrow\widehat{BHA}=\widehat{CHA}=90^0\)

\(\Rightarrow BC\perp AH\) hay \(BC\perp AO\)(đpcm)

b) Xét \(\Delta BAE\) và \(\Delta DAB\) có :

\(\widehat{BAD}\) là góc chung

\(\widehat{BDE}=\widehat{ABE}\) ( cùng chắn \(\stackrel\frown{BE}\))

\(\Rightarrow\Delta BAE\sim\Delta DAB\left(g-g\right)\)

\(\Rightarrow\frac{AE}{AB}=\frac{AB}{AD}\)

\(\Leftrightarrow AB^2=AE.AD\) (1)

Xét \(\Delta BAH\) và \(\Delta BOH\) cùng vuông góc tại H có:

\(AB^2=AH.AO\) ( hệ thức lượng trong tam giác vuông) (2)

Từ (1) và (2) \(\Rightarrow AE.AD=AH.AO\) (đpcm)

Answer 2

[Hoàng Xuân Sơn]

2) △OAB vuông tại B có BH là đường cao => AH.AO=BA²

tương tự △ABD vuông tại B có BE là đường cao => AE.AD = AB²

=> AH.AO=AE.AD

3) △OKA ∽ΔOHF => OK.OF=OH.OA=OB^2=OD^2
=> OK/OD=OD/OF
=>  Δ ODK ∽ ΔODF (c.g.c)
=>góc ODF = 90độ
=> FD là tt của (O)