Cho hai đường thẳng tt' và zz' cắt nhau tại A sao cho \(\widehat{tAz}=60^o\)
a,Tính các góc \(\widehat{tAz'},\widehat{zAt',}\widehat{t'Az}\)
b,Vẽ tia phân giác Am của góc\(\widehat{tAz}\)........An của góc\(\widehat{t'Az'}\)
CHỨNG MINH HAI TIA Am,An là 2 tia đối nhau

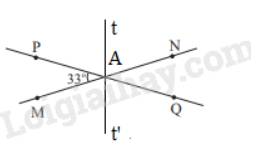
a) Vì zz' cắt tt' tại A
=> tAz = z'At' = 60° ( đối đỉnh)
Mà tAz + tAz' = 180° ( kề bù)
=> tAz' = 180° - 60° = 120°
=> tAz' = zAt' = 120° ( đối đỉnh)
b) Vì Am là phân giác tAz
=> tAM = zAM = \(\frac{60°}{2}=30°\)
Vì An là phân giác z'At'
=> z'AN = t'AN = \(\frac{60°}{2}=30°\)
Mà MAN = MAt + tAz' + z'AN
=> MAN = 30° + 30° + 120°
=> MAN = 180°
=> MAN là góc bẹt
=> AM là tia đối của AN