Tìm m để y = \(\frac{2m+1}{2m-1}.x\)+ 1 đồng biến trên R
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 6 2017
Đáp án A
Phương pháp giải:
Dựa vào điều kiện để hàm số đồng biến hoặc nghịch biến trên khoảng xác định
Lời giải:
Ta có
y
=
x
3
-
3
m
x
2
+
3
(
2
m
-
1
)
x
+
1
R
Hàm số đồng biến trên R 
R 
R
8 tháng 9 2023
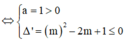
\(y'=\dfrac{1}{3}\cdot3x^2-m\cdot2x+2m+3=x^2-2m\cdot x+2m+3\)
Để hàm số đồng biến trên R thì y'>=0 với mọi x thuộc R
=>Δ=(-2m)^2-4(2m+3)<=0 và 1>0
=>4m^2-8m-12<=0
=>m^2-2m-3<=0
=>(m-3)(m+1)<=0
=>-1<=m<=3
mà m nguyên
nên \(m\in\left\{-1;0;1;2;3\right\}\)
CM
1 tháng 3 2017
Hàm số bậc nhất y = ax + b đồng biến suy ra a > 0 hay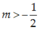 
Chọn D.
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 8 2021
\(y'=3x^2-2\left(2m+1\right)x+m^2+2m=\left(x-m\right)\left(3x-m-2\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}x=m\\x=\dfrac{m+2}{3}\end{matrix}\right.\)
TH1: \(m=\dfrac{m+2}{3}\Rightarrow m=1\) hàm đồng biến trên R (thỏa mãn)
TH2: \(m< \dfrac{m+2}{3}\Rightarrow m< 1\) hàm đồng biến trên khoảng đã cho khi \(\dfrac{m+2}{3}\le0\Rightarrow m\le-2\)
TH3: \(m>\dfrac{m+2}{3}\Rightarrow m>1\) hàm đồng biến trên khoảng đã cho khi \(m\le0\) (ktm)
Vậy \(\left[{}\begin{matrix}m=1\\m\le-2\end{matrix}\right.\)
21 tháng 8 2016
cậu xem đúng thì k y' = x^2 -(2m+1)x+3m+2. Để hs nghịch biến trong 1 khoản có độ dài > 1 thì y'=0 phải có 2 nghiệm phân biệt x1, x2 sao cho |x2-x1| >1 (lúc này thì y' =<0 trong khoản 2 nghiệm [x1, x2] tức là y nghịch biến trong đoạn [x1,x2])
<=> có hệ
(1) y'=0 có 2 nghiệm x1, x2
(2) |x2-x1| > 1 <=> (x2-x1)^2 -1>0 <=> (x1+x2)^2 - 4.x1.x2 -1 >0
21 tháng 8 2016
mk mới hok lớp 8 nên cái tay bó tay!!! ^^
346456454574575675756768797835153453443457657656565
LP
2
29 tháng 8 2021
a)HS đồng biến
`=>2m-1>0`
`=>2m>1=>m>1/2`
b)Gọi điểm cố đính mà hàm số luôn đi qua với mọi m là `A(x_o,y_o)`
`=>y_o=(2m-1).x_o +m-7`
`<=>y_o=2mx_o-x_o +m-7`
`<=>m(2x_o +1)-x_o-y_o-7=0`
`<=>{(2x_o +1=0),(-x_o-y_o-7=0):}`
`<=>x_o=-1/2,y_o=-13/2`
`=>A(-1/2,-13/2)`
Vậy điểm cố đính mà hàm số luôn đi qua với mọi m là `A(-1/2,-13/2)`
29 tháng 8 2021
a: Để hàm số đồng biến thì 2m-1>0
hay \(m>\dfrac{1}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
a.
Hàm là hàm số bậc nhất khi:
\(2m-1\ne0\Leftrightarrow m\ne\dfrac{1}{2}\)
b.
Hàm đồng biến trên R khi:
\(2m-1>0\Leftrightarrow m>\dfrac{1}{2}\)
30 tháng 7 2021
a) Để hàm số là hàm số bậc nhất thì \(2m-1\ne0\)
hay \(m\ne\dfrac{1}{2}\)
b) Để hàm số đồng biến thì 2m-1>0
hay \(m>\dfrac{1}{2}\)
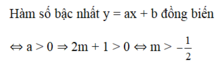
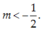
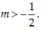
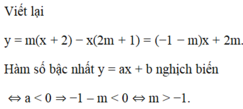
Để hàm số \(y=\frac{2m+1}{2m-1}x+1\) đồng biến trên R
\(\Rightarrow\frac{2m+1}{2m-1}>0\)
TH1: \(\orbr{\begin{cases}2m+1>0\\2m-1>0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}m>-\frac{1}{2}\\m>\frac{1}{2}\end{cases}}\)
\(\Leftrightarrow m>\frac{1}{2}\)
TH2:\(\orbr{\begin{cases}2m+1< 0\\2m-1< 0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}m< -\frac{1}{2}\\m< \frac{1}{2}\end{cases}}\)
\(\Leftrightarrow m< -\frac{1}{2}\)
trong này x không liên quan j ah?