Đề bài: Giải bất phương trình :
a) x2 + 5x + 6 ≥ 0
b) x2 - 9x + 20 ≤ 0
Các cậu giải giúp tớ với, tớ cảm ơn !
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 2 2022
Bài 1:
a: \(\Leftrightarrow x^2-5x+6< =0\)
=>(x-2)(x-3)<=0
=>2<=x<=3
b: \(\Leftrightarrow\left(x-6\right)^2< =0\)
=>x=6
c: \(\Leftrightarrow x^2-2x+1>=0\)
\(\Leftrightarrow\left(x-1\right)^2>=0\)
hay \(x\in R\)
17 tháng 5 2021
`x^2+2x+3>2`
`<=>x^2+2x+1>0`
`<=>(x+1)^2>0`
`<=>x+1 ne 0`
`<=>x ne -1`
`(x+5)(3x^2+2)>0`
Vì `3x^2+2>=2>0`
`=>x+5>0<=>x>-5`
17 tháng 5 2021
c) Ta có: \(21x-10x^2+9< 0\)
\(\Leftrightarrow10x^2-21x-9>0\)
\(\Leftrightarrow x^2-\dfrac{21}{10}x-\dfrac{9}{10}>0\)
\(\Leftrightarrow x^2-2\cdot x\cdot\dfrac{21}{20}+\dfrac{441}{400}>\dfrac{801}{400}\)
\(\Leftrightarrow\left(x-\dfrac{21}{20}\right)^2>\dfrac{801}{400}\)
\(\Leftrightarrow\left[{}\begin{matrix}x>\dfrac{3\sqrt{89}+21}{20}\\x< \dfrac{-3\sqrt{89}+21}{20}\end{matrix}\right.\)
NN
1
12 tháng 2 2023
\(\Leftrightarrow\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}+...+\dfrac{1}{\left(x+5\right)\left(x+6\right)}=\dfrac{1}{8}\)
=>\(\dfrac{1}{x+2}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+4}+...+\dfrac{1}{x+5}-\dfrac{1}{x+6}=\dfrac{1}{8}\)
=>1/x+2-1/x+6=1/8
=>\(\dfrac{x+6-x-2}{\left(x+2\right)\left(x+6\right)}=\dfrac{1}{8}\)
=>x^2+8x+12=32
=>x^2+8x-20=0
=>(x+10)(x-2)=0
=>x=-10 hoặc x=2
PT
1
9 tháng 3 2023
Bài 2:
a: =>2x^2-4x+1=x^2+x+5
=>x^2-5x-4=0
=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)
b: =>11x^2-14x-12=3x^2+4x-7
=>8x^2-18x-5=0
=>x=5/2 hoặc x=-1/4
CM
3 tháng 6 2019
Ta có
g ' ( x ) = ( 2 x + 3 ) . ( x − 2 ) − 1. ( x 2 + 3 x − 9 ) ( x − 2 ) 2 = x 2 − 4 x + 3 ( x − 2 ) 2
Mà g ' ( x ) ≤ 0
⇔ x 2 − 4 x + 3 ≤ 0 x − 2 ≠ 0 ⇔ 1 ≤ x ≤ 3 x ≠ 2 ⇔ x ∈ 1 ; 3 \ 2
Vậy tập nghiệm bất phương trình là: S=[1 ; 3]\{2}
Chọn đáp án B
LK
1
3 tháng 3 2022
cái này ez mà
a,
\(\dfrac{1}{2}x\)\(-3>0\)
\(\Leftrightarrow\dfrac{1}{2}x>3\)
\(\Leftrightarrow x>6\)
b,\(-\dfrac{5}{2}-3\ge0\)
\(-\dfrac{5}{2}\ge3\)
\(x\ge-\dfrac{6}{5}\)
PT
1
CM
18 tháng 7 2019
a) 1,2x3 – x2 – 0,2x = 0
⇔ 0,2x.(6x2 – 5x – 1) = 0
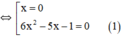
Giải (1): 6x2 – 5x – 1 = 0
có a = 6; b = -5; c = -1
⇒ a + b + c = 0
⇒ (1) có hai nghiệm x1 = 1 và x2 = c/a = -1/6.
Vậy phương trình ban đầu có tập nghiệm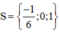 
b) 5x3 – x2 – 5x + 1 = 0
⇔ x2(5x – 1) – (5x – 1) = 0
⇔ (x2 – 1)(5x – 1) = 0
⇔ (x – 1)(x + 1)(5x – 1) = 0
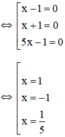
Vậy phương trình có tập nghiệm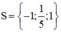 
Đề bài: Giải bất phương trình :
a) x2 + 5x + 6 ≥ 0
⇔x2+5x ≥ -6
⇔x(x+5) ≥ -6
⇔ x ≥ -6 hoặc x+5 ≥ -6
⇔x ≥ -6 hoặc x ≥ -11
b) x2 - 9x + 20 ≤ 0
⇔x(x-9) ≤ -20
⇔ x ≤ 20 hoặc x-9 ≤ - 20
⇔ x ≤ 20 hoặc x ≤ -11
Thấy đúng thì tick nha
a) \(x^2+5x+6\ge0\)
\(\Leftrightarrow x\left(x+5\right)\ge-6\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge-6\\x+5\ge-6\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge-6\\x\ge-11\end{matrix}\right.\)
\(\Leftrightarrow x\ge-6\)
b) \(x^2-9x+20\le0\)
\(\Leftrightarrow x\left(x-9\right)\le-20\)
\(\Leftrightarrow\left[{}\begin{matrix}x\le-20\\x-9\le-20\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\le-20\\x\le-11\end{matrix}\right.\)
\(\Leftrightarrow x\le-20\)