Cho hình bình hành ABCD. Vẽ các \(\Delta ABE;\Delta ADF\)đều nằm ngoài hình bình hành. Gọi M, I, và K là trung điểm của BD, AF và AE. Tính \(\widehat{IMK}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 6 2017
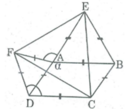
Vì ∠ (BAD) + ∠ (BAE) + ∠ (EAF) + ∠ (FAD) = 360 0
⇒ ∠ (EAF) = 360 0 – ( ∠ (BAD) + ∠ (BAE) + ∠ (FAD) )
Mà ∠ (BAD) = α 2 (gt)
∠ (BAE) = 60 0 (ΔBAE đều)
∠ (FAD) = 60 0 (ΔFAD đều)
Nên ∠ (EAF) = 360 0 – ( α 2 + 60 0 + 60 0 ) = 240 0 – α
CM
5 tháng 7 2018
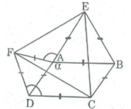
Ta có:
∠ (BAD) + ∠ ∠ (ADC) = 180 0 (hai góc trong cùng phía bù nhau)
⇒ ∠ (ADC) = 180 0 - ∠ (BAD) = 180 0 – α
∠ (CDF) = ∠ (ADC) + ∠ (ADF) = 180 0 - α 2 + 60 0 = 240 0 - α
Suy ra: ∠ (CDF) = ∠ (EAF)
Xét ∆ AEF và ∆ DCF: AF = DF ( vì ∆ ADF đều)
AE = DC (vì cùng bằng AB)
∠ (CDF) = ∠ (EAF) (chứng minh trên)
Do đó: ∆ AEF = ∆ DCF (c.g.c) ⇒ EF = CF (1)
∠ (CBE) = ∠ (ABC) + 60 0 = 180 0 - α + 60 0 = 240 0 - α
Xét ΔBCE và ΔDFC: BE = CD ( vì cùng bằng AB)
∠ (CBE) = ∠ (CDF) = 240 0 - α
BC = DF (vì cùng bằng AD)
Do đó ∆ BCE = ∆ DFC (c.g.c) ⇒ CE = CF (2)
Từ (1) và (2) suy ra: EF = CF = CE
Vậy ∆ ECF đều.
4 tháng 8 2019
a) Vì ABCD là hình bình hành
=> AB = CD ( tính chất)
AD//BC
AB//CD
AD = BC ( tính chất)
BAD = BCD ( tính chất)
Vì E là trung điểm AD
=> AE = ED
Vì F là trung điểm BC
=> BF = FC
Mà AD = BC
AE = ED = BF = FC
Xét ∆ABE và ∆FCD ta có :
AB = CD
AE = BF (cmt)
BAD = FCD ( cmt)
=> ∆ABE = ∆FCD (c.g.c)
b) Vì E\(\in\)AD
F \(\in\)BC
Mà AD//BC
=> ED//BF
Mà ED = BF ( cmt)
=> EBFD là hình bình hành ( dấu hiệu nhận biết)
c) Vì ABCD là hình bình hành
=> AC và BD là 2 đường chéo cắt nhau tại trung điểm mỗi đường
Hay AC và BD cắt nhau tại trung điểm BD (1)
Vì EBCD là hình bình hành
=> BD và FE là 2 đường chéo cắt nhau tại trung điểm mỗi đường
Hay FE và BD cắt nhau tại trung điểm BD (2)
Từ (1) và (2) => AC , BD , FE cắt nhau tại trung điểm BD
=> AC,BD ,FE đồng quy
10 tháng 9 2017
Tính góc EAF
EAF^ = 360* - (DAF^ + BAD^ + BAE^) = 360* - (60* + a + 60*) = 240* - a (1)
b) Chứng minh rằng tam giác CEF là tam giác đều
ABC^ = ADC^ = 180* - a
=> CDF^ = ADC^ + ADF^ = 180* - a + 60* = 240* - a (2)
CBE^ = ABC^ + ABE^ = 180* - a + 60* = 240* - a (3)
AF = DF = AD = BC (4)
CD = AB = BE = AE (5)
(1) (2) (3) (4) và (5) => Δ CDF = ΔEBC = Δ EAF ( c.g.c)
=> CF = CE = EF => CEF là tam giác đều
Tui chịu
K có đủ giữ liệu
Mới chả có góc nào thì tính kiểu j
Nếu ai k sai thì phải giải cho tui xem đóa
Câu hỏi của Hoàng Ngọc Huyền - Toán lớp 8 - Học toán với OnlineMath
Ban tham khao nha !