Tính các giá trị tương ứng của s khi cho t lần lượt lấy các giá trị 1 giờ; 2 giờ; 3 giờ; 4 giờ; … rồi giải thích tại sao s là hàm số của t ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 7 2019
Với t = 1, ta có s = 50.t - 8 = 50.1-8 = 42 (km)
Với t = 2, ta có s = 50.t - 8 = 50.2-8 = 92 (km)
Với t = 3, ta có s = 50.t - 8 = 50.3-8 = 142 (km)
Với t = 4, ta có s = 50.t - 8 = 50.4-8 = 92 (km)
.......
s là hàm số của t vì đại lượng s phụ thuộc vào đại lượng thay đổi t và với mỗi giá trị của t ta chỉ xác định được một giá trị tương ứng của s.
CM
3 tháng 2 2019
Với t = 1, ta có s = 50.t - 8 = 50.1-8 = 42 (km)
Với t = 2, ta có s = 50.t - 8 = 50.2-8 = 92 (km)
Với t = 3, ta có s = 50.t - 8 = 50.3-8 = 142 (km)
Với t = 4, ta có s = 50.t - 8 = 50.4-8 = 92 (km)
.......
s là hàm số của t vì đại lượng s phụ thuộc vào đại lượng thay đổi t và với mỗi giá trị của t ta chỉ xác định được một giá trị tương ứng của s.
15 tháng 8 2023
a: Khi x=-1 thì \(y=2^{-1}=\dfrac{1}{2}\)
Khi x=0 thì \(y=2^0=1\)
Khi x=1 thì \(y=2^1=2\)
Với mỗi giá trị của x thì chỉ có 1 giá trị 2x tương ứng
b: Biểu thức y=2x có nghĩa với mọi x
HQ
Hà Quang Minh
Giáo viên
11 tháng 9 2023
\(v = 10 \Rightarrow t\left( {10} \right) = \dfrac{{20}}{{10}} = 2\);
\(v = 20 \Rightarrow t\left( {20} \right) = \dfrac{{20}}{{20}} = 1\);
\(v = 40 \Rightarrow t\left( {40} \right) = \dfrac{{20}}{{40}} = 0,5\);
\(v = 80 \Rightarrow t\left( {80} \right) = \dfrac{{20}}{{80}} = 0,25\).
Ta lập được bảng sau:
\(v\) | 10 | 20 | 40 | 80 |
t | 2 | 1 | 0,5 | 0,25 |
HQ
Hà Quang Minh
Giáo viên
11 tháng 9 2023
a) \(f\left( 1 \right) = 3.1 = 3;f\left( { - 2} \right) = 3.\left( { - 2} \right) = - 6;f\left( {\dfrac{1}{3}} \right) = 3.\dfrac{1}{3} = 1\).
b) Ta có: \(f\left( { - 3} \right) = 3.\left( { - 3} \right) = - 9;f\left( { - 1} \right) = 3.\left( { - 1} \right) = - 3\)
\(f\left( 0 \right) = 3.0 = 0;f\left( 2 \right) = 3.2 = 6;f\left( 3 \right) = 3.3 = 9\);
Ta lập được bảng sau
\(x\) | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
\(y\) | –9 | -6 | –3 | 0 | 3 | 6 | 9 |
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
a) Với \(x = 1\) thì \(y = {\log _2}1 = 0\)
Với \(x = 2\) thì \(y = {\log _2}2 = 1\)
Với \(x = 4\) thì \(y = {\log _2}4 = 2\)
b) Biểu thức \(y = {\log _2}x\) có nghĩa khi x > 0.
CM
11 tháng 8 2017
a) Sau khi tính giá trị của mỗi giá trị theo các giá trị của x đã cho ta được bảng sau:
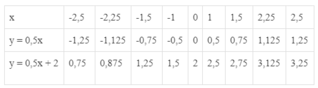
b) Nhận xét: Cùng một giá trị của biến x, giá trị của hàm số y = 0,5x + 2 luôn luôn lớn hơn giá trị tương ứng của hàm số y = 0,5x là 2 đơn vị.
CM
4 tháng 12 2018
| x | -2,5 | -2,25 | -2 | -1,75 | -1,5 | -1,25 | -1 |
| y = f(x) = 1,2x | -3 | -2,7 | -2,4 | -2,1 | -1,8 | -1,5 | -1,2 |
| x | -0,75 | -0,5 | -0,25 | 0 | 0,25 | 0,5 | 0,75 |
| y = f(x) = 1,2x | -0,9 | -0,6 | -0,3 | 0 | 0,3 | 0,6 | 0,9 |
| x | 1 | 1,25 | 1,5 | 1,75 | 2 | 2,25 | 2,5 |
| y = f(x) = 1,2x | 1,2 | 1,5 | 1,8 | 2,1 | 2,4 | 2,7 | 3 |