Cho tam giác nhọn ABC,kẻ 2 đường cao BD và CE.Tia phân giác của các góc ABD và góc ACE cắt nhau tại O,cắt AC và AB lần lượt tại N và M.Tia BN cắt CE tại K,tia CM cắt BD tại H.CMR:
a/\(BN\perp CM\)
b/Tứ giác MNHK là hình thoi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 10 2017
a) Sử dụng tính chất tổng các góc trong một tam giác bằng 1800.
⇒ A B C ^ = A E C ^ ⇒ N B D ^ = M C A ^
Trong DDBN có: N B D ^ + B N D ^ = 90 0
Gọi O = CM Ç BN Þ CM ^ BN = O (1)
b) Xét DCNK có: CO ^ KN Þ CO ^ BN, CO là phân giác A C E ^ nên DCNK cân ở C Þ O là trung điểm KN (2).
Tương tự chứng minh được là trung điểm MH (3).
Từ (1),(2) và (3) suy ra MNHK là hình thoi.
13 tháng 11 2019
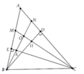
a) Vì tam giác BEC vuông ở E\(\Rightarrow\widehat{B1}+\widehat{B2}+\widehat{B3}+\widehat{C1}=90^0\)( phụ nhau )
Mà \(\widehat{B2}=\widehat{B3}\)( BN là phân giác góc ABD )
\(\Rightarrow\widehat{B1}+2.\widehat{B2}+\widehat{C1}=90^0\left(1\right)\)
Vì tam giác DBC vuông ở D \(\Rightarrow\widehat{C1}+\widehat{C2}+\widehat{C3}+\widehat{B1}=90^0\)( phụ nhau )
Mà \(\widehat{C2}=\widehat{C3}\)( CM là tia phân giác góc ACE)
\(\Rightarrow\widehat{C1}+2.\widehat{C2}++\widehat{B1}=90^0\left(2\right)\)
Lấy \(\left(1\right)+\left(2\right)\)ta được:
\(2.\left(\widehat{B1}+\widehat{C1}\right)+2\left(\widehat{B2}+\widehat{C2}\right)=180^0\)
\(2\left(\widehat{B1}+\widehat{B2}+\widehat{C1}+\widehat{C2}\right)=180^0\)
\(2\left(\widehat{OBC}+\widehat{OCB}\right)=180^0\)
\(\widehat{OBC}+\widehat{OCB}=90^0\)
Xét tam giác OBC có: \(\widehat{OBC}+\widehat{OCB}+\widehat{BOC}=180^0\left(đl\right)\)
\(90^0+\widehat{BOC}=180^0\)
\(\widehat{BOC}=90^0\)
\(\Rightarrow OB\perp OC\)
\(\Rightarrow BN\perp CM\)
b) Vì \(BN\perp CM\left(cmt\right)\)
\(\Rightarrow MH\perp KN\)
Xét tứ giác \(MNHK\)có 2 đường chéo MH và KN vuông góc với nhau
\(\Rightarrow MNHK\)là hình thoi
Theo cái hình này thì mình thấy BN không cắt CE tại một điểm nào đấy khác E đâu bạn. Hơn nữa BN cũng không thể vuông góc với CM do ΔABC nhọn. Bạn xem lại đề giúp mình nha :D