Cho tam giác ABC vuông tại A có góc B=55 độ.Trên nửa mặt phẳng không chứa B , kẻ tia Cx vuông góc với AC.Trên tia Cx lấy điểm D sao cho CD=AB.a. Tính số đo góc ACBb. Chứng minh ΔABC=ΔCDA ;AD song song với BC.c. Kẻ AH vuông góc với BC (H thuộc BC) và CK vuông góc với AD(K thuộc AD).Chứng minh BH=CKd. Gọi I là trung điểm của AC.Chứng minh ba điểm I,K,L thẳng hàngGiúp mik thực hiện bài toán...
Đọc tiếp
Cho tam giác ABC vuông tại A có góc B=55 độ.Trên nửa mặt phẳng không chứa B , kẻ tia Cx vuông góc với AC.Trên tia Cx lấy điểm D sao cho CD=AB.
a. Tính số đo góc ACB
b. Chứng minh
ΔABC=ΔCDA ;AD song song với BC.
c. Kẻ AH vuông góc với BC (H thuộc BC) và CK vuông góc với AD(K thuộc AD).Chứng minh BH=CK
d. Gọi I là trung điểm của AC.Chứng minh ba điểm I,K,L thẳng hàng
Giúp mik thực hiện bài toán này nhé!!!!!
🙊
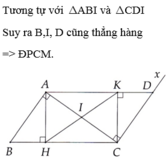
a) Xét t/giác ABC có \(\widehat{A}\) = 900
=> \(\widehat{B}+\widehat{C}=90^0\)
=> \(\widehat{C}=90^0-\widehat{B}=90^0-55^0=35^0\)
b) Xét t/giác ABC và t/giác CAD
có : AB = CD (gt)
\(\widehat{BAC}=\widehat{ACD}=90^0\) (gt)
AC : chung
=> t/giác ABC = t/giác CAD (c.g.c)
=> \(\widehat{BCA}=\widehat{CAD}\) (2 góc t/ứng)
Mà 2 góc này ở vị trí so le trong
=> AD // BC
c) Xét t/giác HAB và t/giác KCD
có: \(\widehat{BHA}=\widehat{CKD}=90^0\) (gt)
AB = CD (gt)
\(\widehat{B}=\widehat{D}\) (vì t/giác ABC = t/giác CDA)
=> t/giác HAB = t/giác KCD (ch - gn)
=> BH = KD (2 cạnh t/ứng) (xem lại đề)
d) Ta có: BH + HC = BC
AK + KD = AD
Mà BH = KD (cmt); BC =AD (vì t/giác ABC = t/giác CDA)
=> HC = AK
Xét t/giác AIK và t/giác CIH
có: AI = IC (gt)
\(\widehat{KAI}=\widehat{ICH}\)(vì t/giác ABC = t/giác CDA)
AK = CH (cmt)
=> t/giác AIK = t/giác CIH (c.g.c)
=> \(\widehat{AIK}=\widehat{HIC}\)(2 góc t/ứng)
Mà \(\widehat{AIH}+\widehat{HIC}=180^0\)(kề bù)
hay \(\widehat{AIK}+\widehat{AIH}=180^0\)
=> ba điểm H, I, K thẳng hàng (xem lại đề)
Cảm ơn bạn Edogawa Conan , mình được 9 điểm nhé ! :)