Tứ giác ABCD có đường chéo AC và BD vuông góc vói nhau . Gọi M; N; L lần lượt là trung điểm của AB AD và đường chéo AC. Từ M kẻ đường thẳng vuông góc với CD cắt AC tại H. Chứng minh : H là trực tâm của tam giác MNL
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Xét tam giác ABC có M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác .
Suy ra: MN// AC và
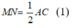
* Xét tam giác ACD có P và Q lần lượt là trung điểm của CD và AD nên PQ là đường trung bình của tam giác
Suy ra: PQ // AC và
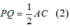
Từ (1) và (2) suy ra: MN// PQ và MN = PQ
Do đó, tứ giác MNPQ là hình bình hành.
* Ta có
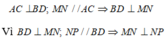
Hình bình hành MNPQ có 1 góc vuông nên là hình chữ nhật
Chọn đáp án C

Gọi K là giao của MI và AD
góc CIM=góc IAM+góc IMA
ΔBIC vuông tạiI có IM là trung tuyến
nên góc CIM=góc ICM=góc ACB
=>góc KAM+góc AMK=góc DAC+góc IAM+góc IMA
=90 độ
=>MI vuông góc AD

a: Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình của ΔABD
Suy ra: MQ//BD và \(MQ=\dfrac{BD}{2}\left(1\right)\)
Xét ΔBCD có
N là trung điểm của BC
P là trung điểm của CD
Do đó: NP là đường trung bình của ΔBCD
Suy ra: NP//BD và \(NP=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra MQ//NP và MQ=NP
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC
mà AC\(\perp\)BD
nên MN\(\perp\)BD
hay MN\(\perp\)MQ
Xét tứ giác MQPN có
MQ//NP
MQ=NP
Do đó: MQPN là hình bình hành
mà \(\widehat{QMN}=90^0\)
nên MQPN là hình chữ nhật

A B C D M N P Q
Xét t/g ABD có: AM=BM (gt), AQ=DQ (gt)
=>MQ là đường trung bình của tam giác ABD
=>MQ // BD và MQ = 1/2BD (1)
CM tương tự với t/g CBD ta có: NP // BD và NP = 1/2BD (2)
Từ (1) và (2) => MQ // NP và MQ = NP
=> MNPQ là hình bình hành (3)
Xét t/g ABC ta có: AM=BM (gt), BN = CN (gt)
=> MN là đg trung bình của t/g ABC
=> MN // AC
Mà AC _|_ BD (gt)
=> MN _|_ BD
Mà NP // BD (cmt)
=> MN _|_ NP (4)
Từ (3) và (4) => MNPQ là hình chữ nhật