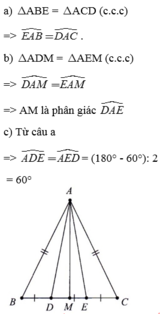
BÀI 1: Cho tam giác ABC có AB=AC. D,E thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE.
a. Chứng minh EAB = DAC.
b. Gọi M là trung điểm của BC. Chứng minh AM là phân giác của DAE.
c. Giả sử DAE = 600. Tính các góc còn lại của tam giác DAE.
BÀI 2: Cho tam giác ABC có A = 900. Vẽ AD vuông góc với AB ( D,C nằm khác phía đối với AB) và AD = AB. Vẽ AE vuông góc với AC (E, B nằm khác phía đối với AC) và AE = AC. Biết DE = BC. Tính BAC.
BÀI 3: Cho tam giác ABC có AB= AC. Kẻ AE là phân giác của góc BAC (E thuộc BC). Chứng minh rằng:
a. Tam giác ABE = tam giác ACE
b. AE là đường trung trực của đoạn thẳng BC.

Bài 1) .
Ta có : AB =AC ( gt)
=> ∆ABC cân tại A
=> B = C
Xét ∆ ABE và ∆ ACD ta có
AD = DE ( gt)
AB = AC ( gt)
B = C ( cmt)
=> ∆ABE = ∆ACD ( c.g.c)
=> EAB = DAC (dpcm)
b) Vì M là trung điểm BC
=> BM = MC
Mà ∆ABC cân tại A ( cmt)
=> AM là trung tuyến ∆ABC
=> AM là trung tuyến đồng thời là đường cao và phân giác ∆ABC
Mà D,E thuộc BC
AM vuông góc với DE
Mà ∆ADE cân tại A ( AD = AE )
=> AM là đường cao đồng thời là phân giác và trung tuyến ∆ ADE
=> AM là phân giác DAE
c) Vì AM là phân giác DAE
=> DAM = EAM = 60/2 = 30 độ
= > Mà AM vuông góc với DE (cmt)
=> AME = AMD = 90 độ
=> AME + MAE + AEM = 180 độ
=> AEM = 180 - 90 - 30 = 60 độ
Mà ∆ADE cân tại A
=> ADE = AED = 60 độ
Bài 2)
Trong ∆ABC có A = 90 độ
=> BAC = 90 độ :))))))