Tìm x,y biết x/y = 2/5 và x.y=70
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
3 tháng 3 2020
Ta có : x:2 = y:5 và x + y = 70
=> x / 2 = y / 5 và x + y = 70
Áp dụng tính chất dãy tỉ số bằng nhau ,ta có :
x / 2 = y / 5 = x + y / 2 + 5 = 70 / 7 = 10
\(\Rightarrow\hept{\begin{cases}x=10.2=20\\y=10.5=50\end{cases}}\)
3 tháng 3 2020
Có \(\frac{x}{y}=\frac{2}{5}\Leftrightarrow\frac{x}{2}=\frac{y}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{2}=\frac{y}{5}=\frac{x+y}{2+5}=\frac{70}{10}=7\)
\(\Leftrightarrow\hept{\begin{cases}x=2\cdot7=14\\y=5\cdot7=35\end{cases}}\)
24 tháng 1 2021
a, \(xy=5\)hay \(x;y\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
| x | 1 | -1 | 5 | -5 |
| y | 5 | -5 | 1 | -1 |
c, \(\left(x+1\right)\left(y-5\right)=-5\)hay \(x+1;y-5\inƯ\left(-5\right)=\left\{\pm1;\pm5\right\}\)
tự lập bảng, tương tự với mấy bài khác chỉ khác nó có điều kiện thì xét nó rồi kết luận nhé!
HA
8 tháng 1 2020
\(x.y=-5\)
\(\Leftrightarrow x.y=-5=-1.5=1.\left(-5\right)=5.\left(-1\right)=-5.1\)
th1\(\orbr{\begin{cases}x=-1\\y=5\end{cases}}\)
th2\(\orbr{\begin{cases}x=1\\y=-5\end{cases}}\)
th3\(\orbr{\begin{cases}x=5\\y=-1\end{cases}}\)
th4\(\orbr{\begin{cases}x=-5\\y=1\end{cases}}\)
NH
13 tháng 2 2020
a) -3n + 2 \(⋮\)2n + 1
<=> 2(-3n + 2) \(⋮\)2n + 1
<=> -6n + 4 \(⋮\)2n + 1
<=> -3(2n + 1) + 7 \(⋮\)2n + 1
<=> 7 \(⋮\)2n + 1
<=> 2n + 1 \(\in\)Ư(7) = {\(\pm\)1; \(\pm\)7}
Lập bảng:
| 2n + 1 | -1 | 1 | -7 | 7 |
| n | -1 | 0 | -4 | 3 |
Vậy n = {-1; 0; -4; 3}
b) n2 - 5n +7 \(⋮\)n - 5
<=> n(n - 5) + 7 \(⋮\)n - 5
<=> 7 \(⋮\)n - 5
<=> n - 5 \(\in\)Ư(7) = {\(\pm\)1; \(\pm\)7}
Lập bảng:
| n - 5 | -1 | 1 | -7 | 7 |
| n | 4 | 6 | -2 | 12 |
Vậy n = {4; 6; -2; 12}
c) (3 - x)(xy + 5) = -1
<=> (3 - x) và (xy + 5) \(\in\)Ư(-1)
Ta có: Ư(-1) \(\in\){-1; 1}
Lập bảng:
| 3 - x | -1 | 1 |
| x | -4 | 2 |
| xy + 5 | 1 | -1 |
| y | 1 | -3 |
Vậy các cặp số (x; y) thỏa mãn lần lượt là (-4; 1) và (2; -3)
d) xy - 3x = 5
<=> x(y - 3) = 5
<=> x và y - 3 \(\in\)Ư(5)
Ta có: Ư(5) \(\in\){\(\pm\)1; \(\pm\)5}
Lập bảng:
| x | -1 | 1 | -5 | 5 |
| y-3 | -5 | 5 | -1 | 1 |
| y | -2 | 8 | 2 | 4 |
Vậy các cặp số (x; y) thỏa mãn lần lượt là (-1; -2); (1; 8); (-5; 2) và (5; 4)
e) xy - 2y + x = -5
<=> y(x - 2) + (x - 2) = -7
<=> (x - 2)(y + 1) = -7
<=> (x - 2) và (y + 1) \(\in\)Ư(-7)
Ta có: Ư(-7) \(\in\){\(\pm\)1; \(\pm\)7}
Lập bảng:
| x - 2 | -1 | 1 | -7 | 7 |
| x | 1 | 3 | -5 | 9 |
| y + 1 | 7 | -7 | 1 | -1 |
| y | 6 | -8 | 0 | -2 |
Vậy các cặp số (x; y) thỏa mãn lần lượt là (1; 6): (3; -8); (-5; 0) và (9; -2)
14 tháng 5 2023
phương trình nghiệm nguyên kiểu này liệt kê ước rồi kẻ bảng ra nhé
QV
2
10 tháng 3 2016
x(y+3)+2(y+3)=0
(x+2).(y+3)=0
x+2=0 hoặc y+3=0
x=-2 hoặc y=-3 thỏa man:|-2|+|-3|=5
20 tháng 10 2021
Bài 2:
Đặt \(\dfrac{x}{3}=\dfrac{y}{4}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k\\y=4k\end{matrix}\right.\)
Ta có: xy=12
\(\Leftrightarrow12k^2=12\)
\(\Leftrightarrow k^2=1\)
Trường hợp 1: k=1
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k=3\\y=4k=4\end{matrix}\right.\)
Trường hợp 2: k=-1
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k=-3\\y=4k=-4\end{matrix}\right.\)
11 tháng 12 2014
- Đặt x/2 = y/5 = k ( k khác 0 )
- => x=2k; y=5k (1)
- Thay (1) vào x.y=40, có :
- 2.k.5.k = 40
- 10.k mũ 2 = 40
- k mũ 2 = 40 : 10 = 4
- k = 2 hoặc k= -2
- Nếu k = 2 thì x= 2.2 = 4 ; y = 2.5 = 10
- Nếu k = -2 thì x= -2.2 = -4 ; y= -2.5= -10
- Kết luận ....
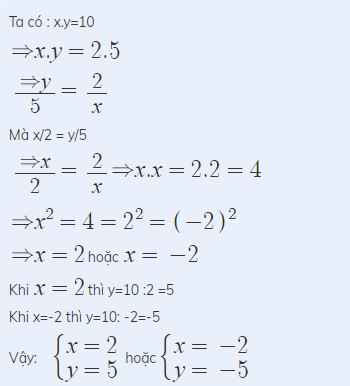
\(\dfrac{x}{y}=\dfrac{2}{5}\Leftrightarrow\dfrac{x}{2}=\dfrac{y}{5}\)
Đặt \(\dfrac{x}{2}=\dfrac{y}{5}=k\Leftrightarrow x=2k;y=5k\)
\(xy=70\Leftrightarrow10k^2=70\Leftrightarrow k^2=7\\ \Leftrightarrow\left[{}\begin{matrix}k=\sqrt{7}\\k=-\sqrt{7}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\sqrt{7};y=5\sqrt{7}\\x=-2\sqrt{7};y=-5\sqrt{7}\end{matrix}\right.\)