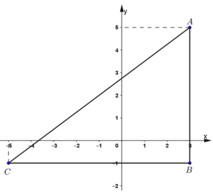
Vẽ tam giác ABC trên mặt phẳng tọa độ biết A(1;2) ; B(-1;0) và C(2;0). Tính SABC ( theo đơn vị đo trên mỗi trục tọa độ)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 6 2021
b) Độ dài đoạn thẳng AB là:
\(AB=\sqrt{\left(2-2\right)^2+\left(4+1\right)^2}=5\)
Độ dài đoạn thẳng AC là:
\(AC=\sqrt{\left(2+4\right)^2+\left(4+1\right)^2}=\sqrt{61}\)
Độ dài đoạn thẳng BC là:
\(BC=\sqrt{\left(2+4\right)^2+\left(-1+1\right)^2}=6\)
Ta có: \(BA^2+BC^2=5^2+6^2=25+36=61\)
\(AC^2=\left(\sqrt{61}\right)^2=61\)
Do đó: \(AC^2=BA^2+BC^2\)(=61)
Xét ΔABC có \(AC^2=BA^2+BC^2\)(cmt)
nên ΔABC vuông tại B(Định lí Pytago đảo)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{BA\cdot BC}{2}=\dfrac{5\cdot6}{2}=\dfrac{30}{2}=15\left(cm^2\right)\)
WR
5 tháng 6 2017
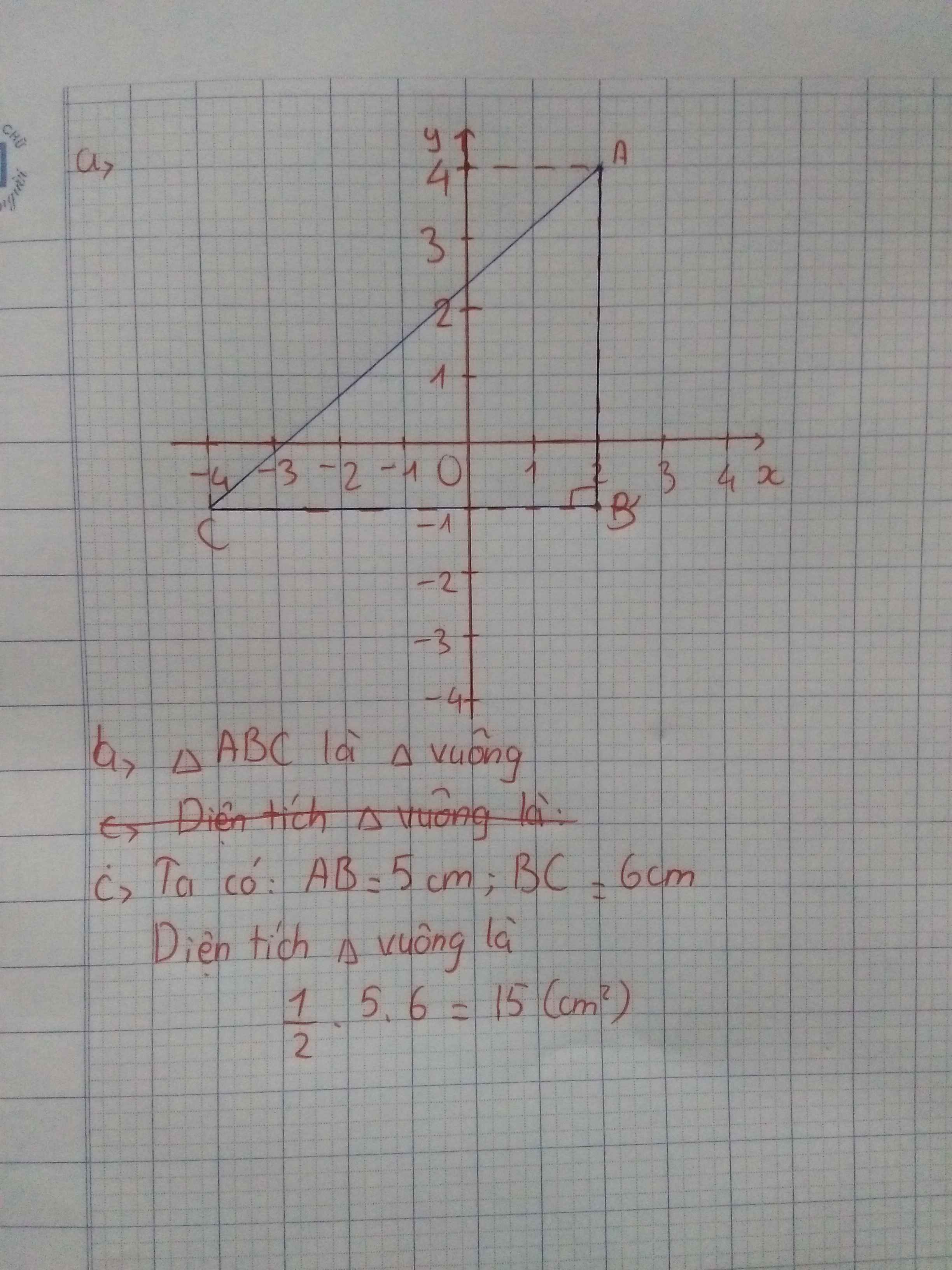
a) hình tự vẽ
b)theo hình vẽ tam giác ABC là tam giác vuông ở B
ta có AB=5,BC=6=>\(SABC=\frac{AB.BC}{2}=\frac{30}{2}=15\)(đơn vị diện tích)
29 tháng 12 2021
a: \(AB=\sqrt{\left[2-\left(-2\right)\right]^2+\left(-1-2\right)^2}=5\)
\(BC=\sqrt{\left(5-2\right)^2+\left(3+1\right)^2}=5\)
Do đó: AB=BC
hay ΔABC cân tại B
Ta có:
BC = BO + OC = \(|-1|+|2|=3\)
=> SABC = \(\frac{1}{2}BC.AH=\frac{1}{2}.3.2=6\)\(\left(đvdt\right)\)