Trên đường thẳng x'x lấy 1 điểm O . Trên nửa mp bờ x'x vẽ tia Oy sao cho xOy = 45^o . Trên nửa mp kia vẽ tia Oy sao cho Oz vuông góc Ox . Gọi Oy' là tia phân giác của x'Oy' . a) Chứng tỏ rằng xOy và x'Oy' là 2 góc đối đỉnh . b) Trên nửa mp bờ x'x có chứa tia Oy , vẽ tia Ot sao cho Ot vuông góc Oy . Tính x'Ot
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Ta có: (d2): \(y=\dfrac{-x}{3}-\dfrac{1}{2}\)
\(\Leftrightarrow y=\dfrac{-1}{3}x-\dfrac{1}{2}\)
Gọi A(xA;yA) là giao điểm của (d1) và (d2)
Hoành độ của A là:
\(\dfrac{-1}{3}x-\dfrac{1}{2}=2-x\)
\(\Leftrightarrow\dfrac{-1}{3}x-\dfrac{1}{2}-2+x=0\)
\(\Leftrightarrow\dfrac{2}{3}x-\dfrac{5}{2}=0\)
\(\Leftrightarrow\dfrac{2}{3}x=\dfrac{5}{2}\)
\(\Leftrightarrow x=\dfrac{5}{2}:\dfrac{2}{3}=\dfrac{5}{2}\cdot\dfrac{3}{2}=\dfrac{15}{4}\)
Thay \(x=\dfrac{15}{4}\) vào hàm số y=2-x, ta được:
\(y=2-\dfrac{15}{4}=\dfrac{8}{4}-\dfrac{15}{4}=-\dfrac{7}{4}\)
Vậy: \(A\left(\dfrac{15}{4};-\dfrac{7}{4}\right)\)

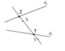
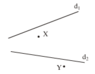
Vì X, Z, T thẳng hàng và Y, Z, T thẳng hàng nên cả 4 điểm này đều nằm trên đường thẳng XY.
Cách vẽ: Vẽ đường thẳng XY cắt d1 tại Z, cắt d2 tại T.

Vì đường thẳng y = (2m - 1)x - 3m + 7 cắt đường thẳng y = x - 1 tại điểm trên trục hoành nên tung độ bằng 0 hay y = 0.
Thay y = 0 vào pt y = x - 1 ta có :
x - 1 = 0 => x = 1
Vậy giao điểm của 2 đt là A( 1; 0)
Thay tọa độ điểm A vào pt đt y = ( 2m -1) x - 3m + 7 ta có :
(2m -1) .1 - 3m + 7 = 0
2m - 1 - 3m + 7 = 0
-m + 6 = 0
m = 6
Kết luận : với m = 6 thì đt y = (2m -1)x - 3m + 7 có dạng :
y = 11x - 11 và cắt đường thẳng y = x - 1 tại 1 điểm trên trục hoành.
lengocanh 2 nửa mp đều có Oy luôn à
Nguyễn Trúc Giang , cảm ơn bạn mk làm dc rồi