Vẽ đồ thị của hàm số \(y=4x^2+3x+6\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1 :
Với x = 1 thì y = 4.1 = 4
Ta được \(A\left(1;4\right)\) thuộc đồ thị hàm số y = f(x) = 4x
Đường thẳng OA là đồ thị hàm số y = f(x) = 4x
a) Ta có : \(f\left(2\right)=4\cdot2=8\)
\(f\left(-2\right)=4\cdot\left(-2\right)=-8\)
\(f\left(4\right)=4\cdot4=16\)
\(f\left(0\right)=4\cdot0=0\)
b) +) y = -1 thì \(4x=-1\) => \(x=-\frac{1}{4}\)
+) y = 0 thì 4x = 0 => x = 0
+) y = 2,5 thì 4x = 2,5 => \(4x=\frac{5}{2}\)=> x = \(\frac{5}{8}\)
Bài 2 :
a) Vẽ tương tự như bài 1
b) Thay \(M\left(-2,6\right)\)vào đths y = -3x ta có :
y =(-3)(-2) = 6
=> Điểm M thuộc đths y = -3x
c) Thay tung độ của P là 5 vào đồ thị hàm số y = -3x ta có :
=> 5 = -3x => \(x=-\frac{5}{3}\)
Vậy tọa độ của điểm P là \(P\left(-\frac{5}{3};5\right)\)

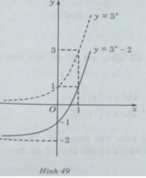
Đồ thị của hàm số y: y = 3 x − 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung xuống dưới 2 đơn vị (H. 49)
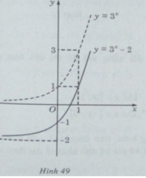

y = 2 – 3 x = −( 3 x − 2)
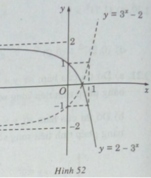
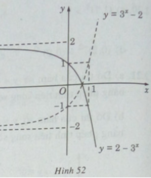
Ta có đồ thị của hàm số y = 2 − 3 x đối xứng với đồ thị cua hàm số y = 3 x – 2 qua trục hoành (H.52).

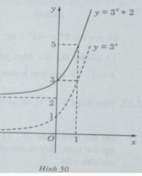
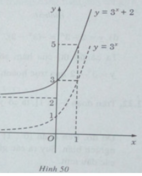
Đồ thị của hàm số y = 3 x + 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung lên phía trên 2 đơn vị (H. 50)

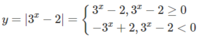
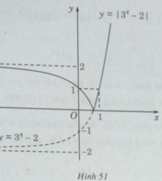
Do đó, đồ thị của hàm số y = | 3 x − 2| gồm:
- Phần đồ thị của hàm số y = 3 x − 2 ứng với 3 x – 2 ≥ 0 (nằm phía trên trục hoành).
- Phần đối xứng qua trục hoành của đồ thị hàm số y = 3 x − 2 ứng với 3 x – 2 < 0.
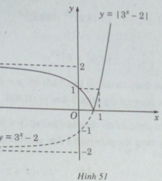
Vậy đồ thị của hàm số y = | 3 x − 2| có dạng như hình 51.

a) Đồ thị của hàm số y: y = 3 x − 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung xuống dưới 2 đơn vị (H. 49)
b) Đồ thị của hàm số y = 3 x + 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung lên phía trên 2 đơn vị (H. 50)
c) 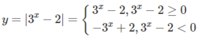
Do đó, đồ thị của hàm số y = | 3 x − 2| gồm:
- Phần đồ thị của hàm số y = 3 x − 2 ứng với 3 x – 2 ≥ 0 (nằm phía trên trục hoành).
- Phần đối xứng qua trục hoành của đồ thị hàm số y = 3 x − 2 ứng với 3 x – 2 < 0.
Vậy đồ thị của hàm số y = | 3 x − 2| có dạng như hình 51.
Ta có đồ thị của hàm số y = 2 − 3 x đối xứng với đồ thị cua hàm số y = 3 x – 2 qua trục hoành (H.52).

Tham khảo:
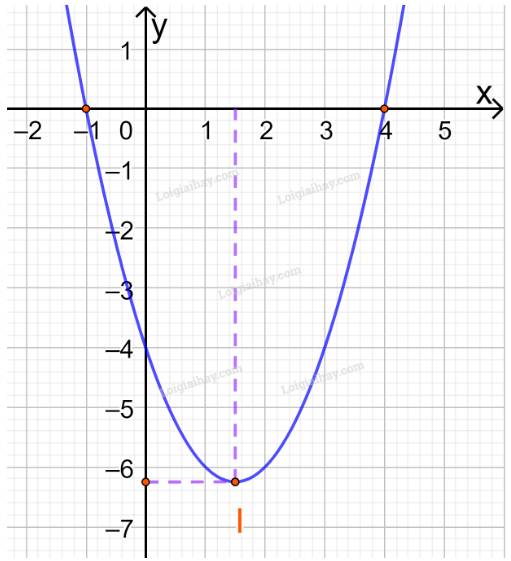
a) \(y = {x^2} - 3x - 4\)
Đồ thị hàm số có đỉnh \(I\left( {\dfrac{3}{2}; - \dfrac{{25}}{4}} \right)\)
Trục đối xứng là \(x = \dfrac{3}{2}\)
Giao điểm của parabol với trục tung là (0;-4)
Giao điểm của parabol với trục hoành là (-1;0) và (4;0)
Điểm đối xứng với điểm (0;-4) qua trục đối xứng \(x = \frac{3}{2}\) là (3;-4)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
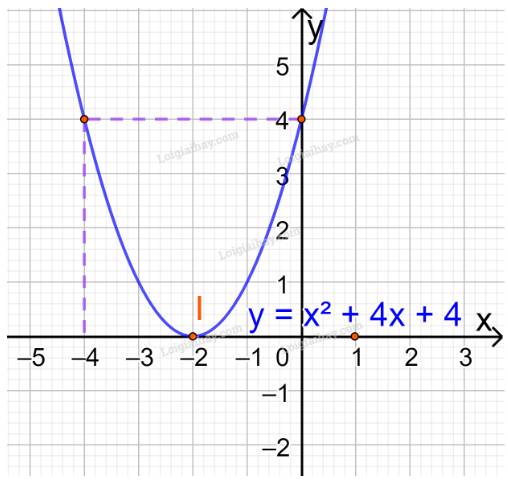
b) \(y = {x^2} + 4x + 4\)
Đồ thị hàm số có đỉnh \(I\left( { - 2;0} \right)\)
Trục đối xứng là \(x = - 2\)
Giao điểm của parabol với trục tung là (0;4)
Giao điểm của parabol với trục hoành là I(-2;0)
Điểm đối xứng với điểm (0;4) qua trục đối xứng \(x = - 2\) là (-4;4)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
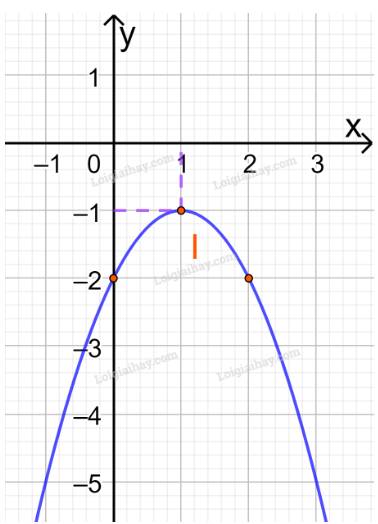
c) \(y = - {x^2} + 2x - 2\)
Đồ thị hàm số có đỉnh \(I\left( {1; - 1} \right)\)
Trục đối xứng là \(x = 1\)
Giao điểm của parabol với trục tung là (0;-2)
Điểm đối xứng với điểm (0;-2) qua trục đối xứng \(x = 1\) là (2;-2)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:

a: 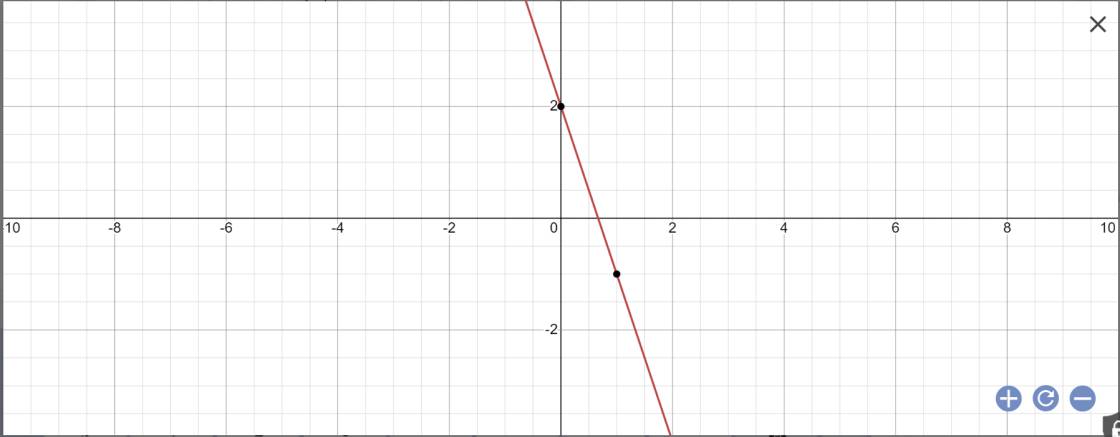
b: Để đồ thị hàm số y=(m+1)x-3 song song với đồ thị hàm số y=-3x+2 thì \(\left\{{}\begin{matrix}m+1=-3\\2\ne-3\left(đúng\right)\end{matrix}\right.\)
=>m+1=-3
=>m=-4
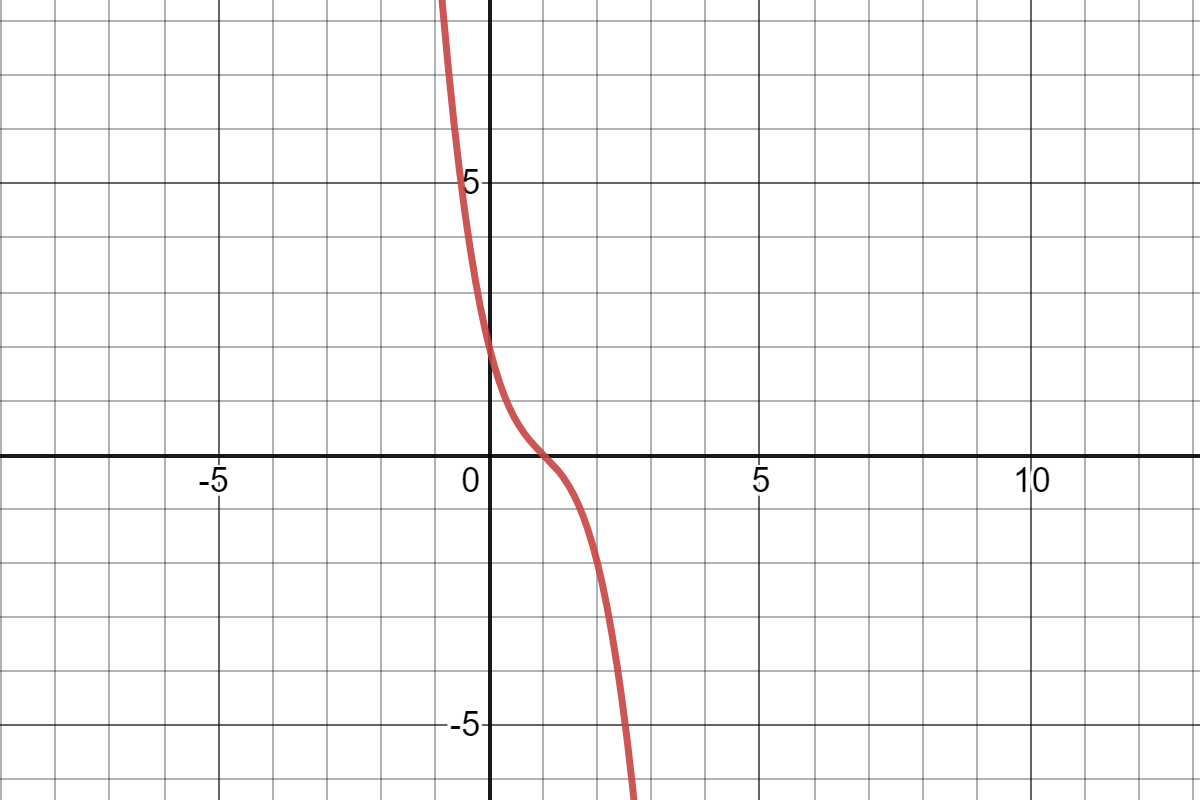

Đồ thị của hàm số đây