Tính:
A=1/1x3 + 1/3x2 + 1/2x5 +...+ 1/49x25
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{1}{1.3}+\frac{1}{3.2}+\frac{1}{2.5}+...+\frac{1}{99.100}\)
= \(2.\left(\frac{1}{1.3.2}+\frac{1}{3.2.2}+\frac{1}{2.5.2}+...+\frac{1}{99.50.2}\right)\)
= \(2.\left(\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{99.100}\right)\)
= \(2.\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{99}-\frac{1}{100}\right)\)
= \(2.\left(\frac{1}{2}-\frac{1}{100}\right)\)
= \(2.\frac{49}{100}\)
= \(\frac{49}{50}\)

\(\dfrac{1}{1.3}+\dfrac{1}{2.3}+\dfrac{1}{2.5}+\dfrac{1}{3.5}+\dfrac{1}{3.7}+\dfrac{1}{4.7}+\dfrac{1}{4.9}\)
\(=\dfrac{1}{1.3}+\dfrac{1}{3.2}+\dfrac{1}{2.5}+\dfrac{1}{5.3}+\dfrac{1}{3.7}+\dfrac{1}{7.4}+\dfrac{1}{4.9}\)
\(=\left(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}\right):\dfrac{1}{2}\)
\(=\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}\right):\dfrac{1}{2}\)
\(=\left(\dfrac{1}{2}-\dfrac{1}{9}\right):\dfrac{1}{2}\)
\(=\dfrac{7}{18}:\dfrac{1}{2}\)
\(=\dfrac{7}{9}\)

2 x - 1 + 2 x + 3 x 2 + x + 1 = 2 x - 1 2 x + 1 x 3 - 1 Đ K X Đ : x ≠ 1 ⇔ 2 x 2 + x + 1 x 3 - 1 + 2 x + 3 x - 1 x 3 - 1 = 2 x - 1 2 x + 1 x 3 - 1
⇔ 2( x 2 + x + 1) + (2x + 3)(x – 1) = (2x – 1)(2x + 1)
⇔ 2 x 2 + 2x + 2 + 2 x 2 – 2x + 3x – 3 = 4 x 2 – 1
⇔ 2 x 2 + 2 x 2 – 4 x 2 + 2x – 2x + 3x = -1 – 2 + 3
⇔ 3x = 0 ⇔ x = 0 (thỏa mãn)
Vậy phương trình có nghiệm x = 0.

Bài 1:
\(a,=6x^2+6x\\ b,=15x^3-10x^2+5x\\ c,=6x^3+12x^2\\ d,=15x^4+20x^3-5x^2\\ e,=2x^2+3x-2x-3=2x^2+x-3\\ f,=3x^2-5x+6x-10=3x^2+x-10\)
Bài 2:
\(a,\Leftrightarrow3x^2+3x-3x^2=6\\ \Leftrightarrow3x=6\Leftrightarrow x=2\\ b,\Leftrightarrow6x^2+3x-6x^2+9x-2x-3=10\\ \Leftrightarrow10x=13\Leftrightarrow x=\dfrac{13}{10}\)

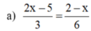
![]()
⇔ 4x - 10 = 2 - x
⇔ 4x + x = 2 + 10 ⇔ 5x = 12 ⇔ x = 12/5
Vậy: S = {12/5}
b) (3x + 1) = (3x + 1)2
⇔ (3x + 1)2 - (3x + 1) = 0
⇔ (3x + 1)[(3x + 1) - 1] = 0
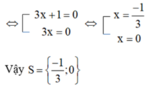
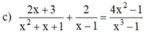
ĐKXĐ:x ≠ 1
Quy đồng mẫu hai vế của phương trình ta được:
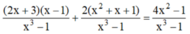
Khử mẫu hai vế, ta được:
(2x + 3)(x - 1) + 2(x2 + x + 1) = 4x2 - 1
⇔ 2x2 + x - 3 + 2x2 + 2x + 2 = 4x2 - 1
⇔ 3x - 1 = -1
⇔ 3x = 0 ⇔ x = 0 (thỏa mãn điều kiện)
Vậy: S = {0}

a,A = \(\dfrac{3x^2+6xy}{6x^2}\) (đk \(x\) ≠ 0)
A = \(\dfrac{3x.\left(x+2y\right)}{6x^2}\)
A = \(\dfrac{x+2y}{2x}\)
b,B = \(\dfrac{2x^2-x^3}{x^2-4}\) (đk \(x\)2 - 4 ≠ 0 ⇒ \(x\) ≠ \(\pm\) 2)
B = \(\dfrac{x^2\left(2-x\right)}{\left(x+2\right)\left(x-2\right)}\)
B = \(\dfrac{-x^2.\left(x-2\right)}{\left(x+2\right).\left(x-2\right)}\)
B = \(\dfrac{-x^2}{x+2}\)

a=511/256
b=647/20
c=mình đang suy nghĩ,nhưng nếu bạn k cho mình thì bạn sẽ có câu trả lời
a. 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256
= 1 + ( 1 - 1/2) + ( 1/2 - 1/4) + ( 1/4 - 1/8) + ( 1/8 - 1/16) + ( 1/16 - 1/32) + (1/32 - 1/64) + ( 1/64 - 1/128) + (1/128 - 1/256)
= 1 + 1 - 1/2 + 1/2 - 1/4 + 1/4 - 1/8 + 1/8 - 1/16 + 1/16 - 1/32 + 1/32 - 1/64 + 1/64 - 1/128 + 1/128 - 1/256
= 2 - 1/256
= 511/256
Câu b bạn có viết sai đề không vậy?
Bạn làm được chưa?