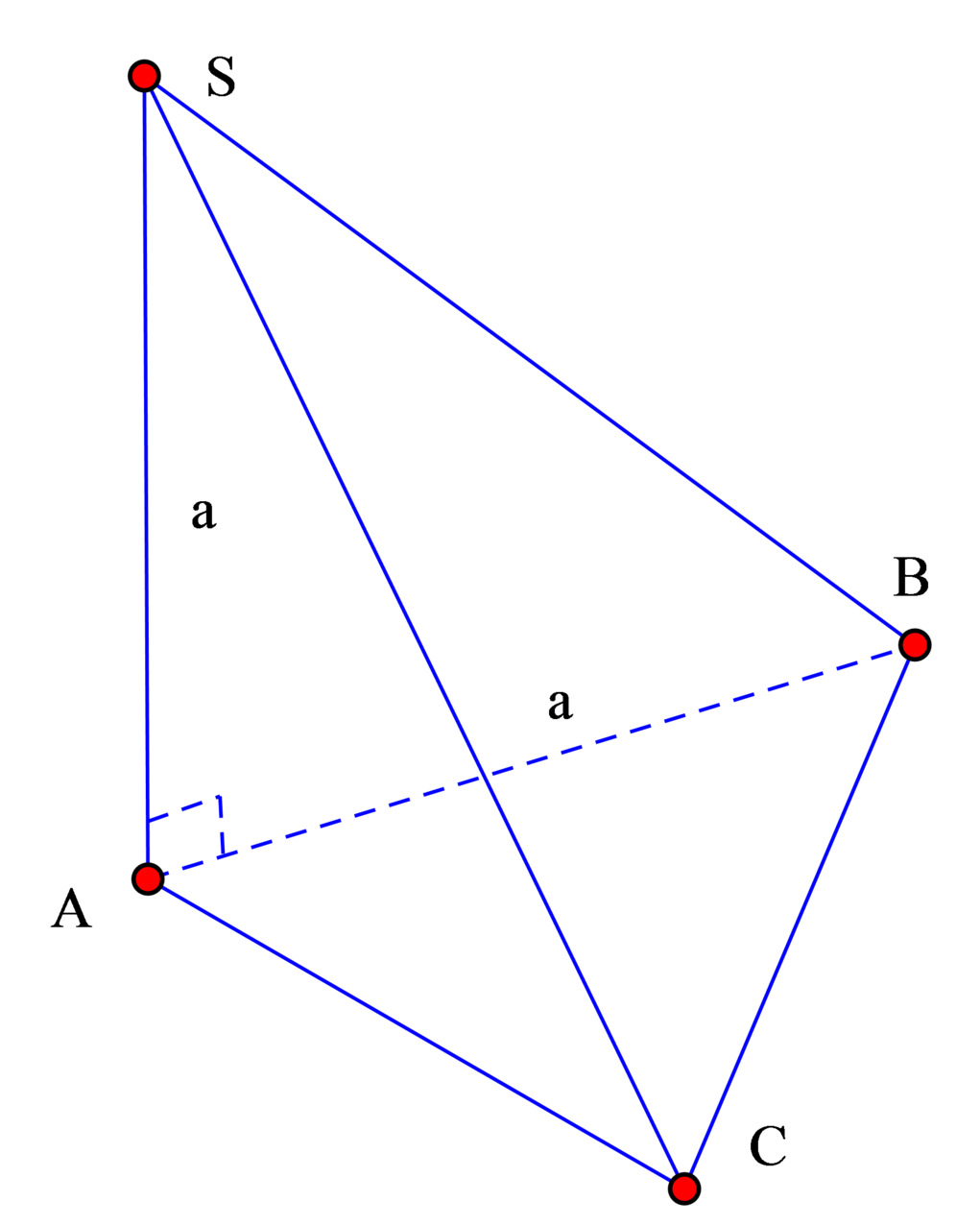
Cho hình chóp S.ABC có tam giác ABC và tam giác SBC là hai tam giác đều cạnh a. SA=a\(\frac{\sqrt{3}}{2}\) .M thuộc AB, AM = b (0<b<a), (P) là mp qua M và vuông góc BC cắt hình chóp S.ABC theo thiết diện.Tính diện tích thiết diện đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Ta có diện tích tam giác đều cạnh a là S = a 2 3 4
⇒ V S . A B C = 1 3 S A . d t A B C = 1 3 a . a 2 3 4 = a 3 3 12

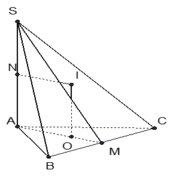
Gọi M là trung điểm SA và O là tâm đáy \(\Rightarrow AO=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\) ; \(AM=\dfrac{a}{2}\)
Qua O kẻ đường thẳng d song song SA, trong mặt phẳng (SAO) qua M kẻ đường thẳng song song AO cắt d tại I
\(\Rightarrow I\) là tâm mặt cầu ngoại tiếp chóp
\(R=IA=\sqrt{IM^2+AM^2}=\sqrt{AO^2+AM^2}=\dfrac{a\sqrt{21}}{6}\)

Đáp án A
Ta có S A B C = a 2 3 4 = 3 4 ⇒ V = 1 3 S A . S A B C = 3 12


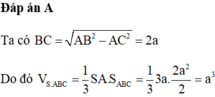
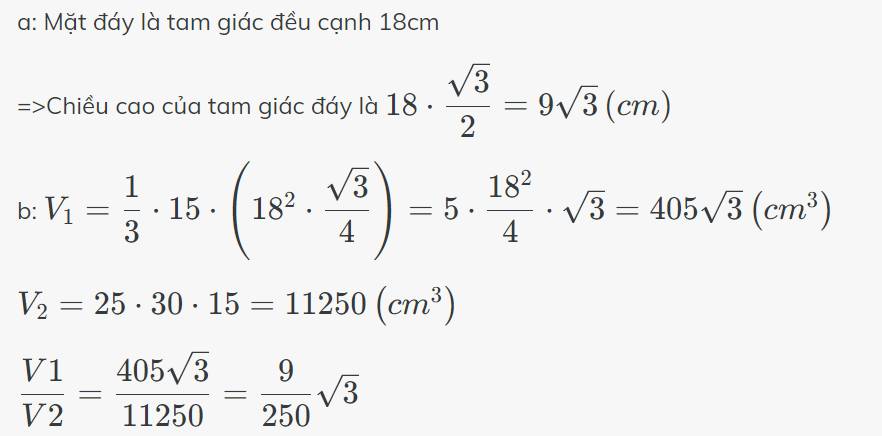
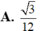
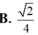
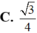
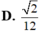
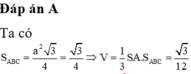

Bạn tự vẽ hình
Gọi N là trung điểm BC \(\Rightarrow AN=\frac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều ABC cạnh a)
\(SN=\frac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều SBC cạnh a)
\(\Rightarrow AN=SN=SA=\frac{a\sqrt{3}}{2}\Rightarrow\Delta SAN\) đều
\(\left\{{}\begin{matrix}BC\perp SN\\BC\perp AN\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAN\right)\)
\(\left(P\right)\perp BC\Rightarrow\left(P\right)//\left(SAN\right)\)
Từ M kẻ \(MD//AN\left(D\in BC\right)\), từ M kẻ \(ME//SA\left(E\in SB\right)\)
\(\Rightarrow\Delta MDE\) là thiết diện của (P) và chóp
Theo đt Talet: \(\frac{MD}{AN}=\frac{ME}{SA}=\frac{DE}{SN}=\frac{BM}{AB}\)
\(\Rightarrow MD=ME=DE=\frac{AN.BM}{AB}=\frac{\frac{a\sqrt{3}}{2}\left(a-b\right)}{a}=\frac{\sqrt{3}}{2}\left(a-b\right)\)
\(\Rightarrow\Delta MDE\) là tam giác đều cạnh \(\frac{\sqrt{3}}{2}\left(a-b\right)\)
Theo công thức diện tích tam giác đều:
\(S_{MDE}=\frac{\left(\frac{\sqrt{3}}{2}\left(a-b\right)\right)^2\sqrt{3}}{4}=\frac{3\sqrt{3}}{16}\left(a-b\right)^2\)