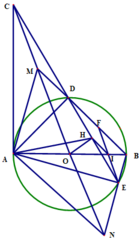
Cho đường tròn (O) đường kính AB=2R. Từ A vẽ hai tia nằm hai bên AB, hai tia này cắt tiếp tuyến tại B của đường tròn (O) ở M và N. AM và AN lần lượt cắt đường tròn (O) ở C và D.
a) Chứng minh: tứ giác CDMN nội tiếp một đường tròn
b) Chứng minh: AC×AM=AD×AN=4R^2
c) Cho góc CAB=30°. Tính diện tích phần mặt phẳng của tam giác ABM nằm ngoài đường tròn (O)