Giúp mình với ạ đề là rút gọn biểu thức
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


d: \(\dfrac{-\left(\sqrt{3}-\sqrt{6}\right)}{1-\sqrt{2}}+\dfrac{6\sqrt{3}+3}{\sqrt{3}}-\dfrac{13}{4+\sqrt{3}}\)
\(=-\sqrt{3}+6+\sqrt{3}-4+\sqrt{3}\)
\(=2+\sqrt{3}\)

\(B=9x^4-\left(2x+1\right)^2-\left(9x^4+6x^2+1\right)\\ =9x^4-4x^2-4x-1-9x^4-6x^2-1\\ =-10x^2-4x-2\)

\(\dfrac{2sin8a-sin16a}{2sin8a+sin16a}=\dfrac{2sin8a-2sin8a.cos8a}{2sin8a+2sin8a.cos8a}=\dfrac{2sin8a\left(1-cos8a\right)}{2sin8a\left(1+cos8a\right)}=\dfrac{1-cos8a}{1+cos8a}=\dfrac{1-\left(1-2sin^24a\right)}{1+\left(1-2sin^24a\right)}=\dfrac{2sin^24a}{2-2sin^24a}=\dfrac{sin^24a}{1-sin^24a}=\dfrac{sin^24a}{cot^24a}=tan^24a\)
\(=\dfrac{2sin8a-2sin8a.cos8a}{2sin8a+2sin8a.cos8a}=\dfrac{2sin8a\left(1-cos8a\right)}{2sin8a\left(1+cos8a\right)}=\dfrac{1-cos8a}{1+cos8a}\)
\(=\dfrac{1-\left(1-2sin^24a\right)}{1+\left(2cos^24a-1\right)}=\dfrac{2sin^24a}{2cos^24a}=tan^24a\)



Sửa đề: \(B=\sqrt{a-1+2\sqrt{a-1}+1}+\sqrt{a-1-2\sqrt{a-1}+1}\)
\(=\sqrt{\left(\sqrt{a-1}+1\right)^2}+\sqrt{\left(\sqrt{a-1}-1\right)^2}\)
\(=\left|\sqrt{a-1}+1\right|+\left|\sqrt{a-1}-1\right|\)
\(=\sqrt{a-1}+1+1-\sqrt{a-1}=2\)

1: \(A=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)-5-\sqrt{x}-3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{x-4-\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}=\dfrac{x-\sqrt{x}-12}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\)

c: \(P=4\left(x-3\right)-3\left|x+3\right|\)
Trường hợp 1: x>=-3
\(P=4x-12-3x-9=x-21\)
Trường hợp 2: x<-3
P=4x-12+3x+9=7x-3
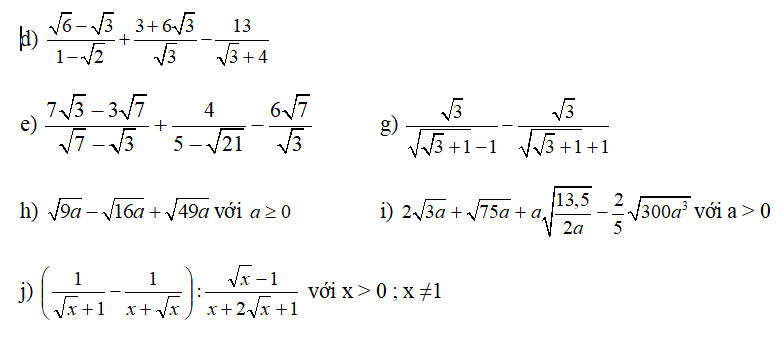



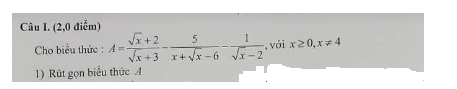 rút gọn biểu thức, giúp e với ạ :<
rút gọn biểu thức, giúp e với ạ :<
a) \(\sqrt{0,64.a^2}\left(a>0\right)=0,8.\left|a\right|=0,8a\)
b) \(\sqrt{a^2\left(a-2\right)^2}\left(a>2\right)=\left|a\left(a-2\right)\right|=a\left(a-2\right)=a^2-2a\)
c) \(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}\left(a\ge0,a\ne1\right)=\dfrac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}{1-\sqrt{a}}=1+\sqrt{a}+a\)