Tìm số tự nhiên m sao cho: 6m chia hết cho 2m – 1.
giúp mình vớiiiiii
huhu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
2
19 tháng 10 2015
2m+18 chia hết cho m+1
=> 2m+2+16 chia hết cho m+1
=> 2.(m+1)+16 chia hết cho m+1
=> 16 chia hết cho m+1
=> m+1\(\in U\left(16\right)\)
Vì m là số tự nhiên
=> m> -1
=> m+1>0
=> m+1=1;2;4;8;16
=> m= 0;1;3;7;15
LC
19 tháng 10 2015
Ta có: 2m+18 chia hết cho m+1
=>2m+2+16 chia hết cho m+1
=>2.(m+1)+16 chia hết cho m+1
=>16 chia hết cho m+1
=>m+1=Ư(16)=(1,2,4,8,16)
=>m=(0,1,3,7,15)
CM
30 tháng 3 2019
Chọn đáp án C.
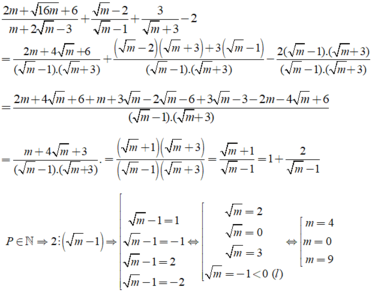
Thử lại, với m= 4 thì P =3 ( thỏa mãn)
Với m = 0 thì P = -1 ( không là số tự nhiên).
Với m = 9 thì P = 2 ( thỏa mãn)
Vậy m = 4 hoặc m = 9.
21 tháng 5 2016
Ta có: n+1 chia hết cho 165
=> n+1 thuộc B(165) = { 0 ; 165;330;495;660.....}
=> n = { -1 ; 164 ; 329 ; 494;659;............}
Vì n chia hết cho 21
=> n =
LP
6
5 tháng 1 2017
2n + 5 chia hết cho n + 1
n +1 chia hết cho n + 1
=> 2( n +1 ) chia hết cho n + 1
=> 2n + 2 chia hết cho n + 1
=> 2n + 5 - 2n - 2 chia hết cho n+1
=. 3 chia hết cho n+ 1
=> n + 1 thuộc ước của 3
AT
2
LM
10 tháng 10 2021
6m⋮2m−16m⋮2m−1
⇔2m−1∈{−1;1;3}⇔2m−1∈{−1;1;3}
⇔2m∈{0;2;4}⇔2m∈{0;2;4}
hay m∈{0;1;2}
^HT^
HD
1
7 tháng 12 2015
n + 5 chia hết cho n + 1
n + 1 + 4 chia hết cho n + 1
4 chia hết cho n + 1
n + 1 thuộc Ư(4) = [1;2;4}
n thuộc {0 ; 1 ; 3}
AH
Akai Haruma
Giáo viên
17 tháng 12 2023
Lời giải:
$n^3+3n+1\vdots n+1$
$\Rightarrow (n^3+1)+3n\vdots n+1$
$\Rightarrow (n+1)(n^2-n+1)+3(n+1)-3\vdots n+1$
$\Rightarrow (n+1)(n^2-n+4)-3\vdots n+1$
$\Rightarrow 3\vdots n+1$
$\Rightarrow n+1\in \left\{1; 3\right\}$ (do $n+1$ là stn)
$\Rightarrow n\in \left\{0; 2\right\}$
\(6m⋮2m-1\)
\(\Leftrightarrow2m-1\in\left\{-1;1;3\right\}\)
\(\Leftrightarrow2m\in\left\{0;2;4\right\}\)
hay \(m\in\left\{0;1;2\right\}\)
m = 5