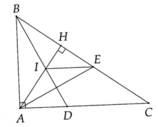
Cho tam giác EMN cân tại E ( góc E < \(^{90^0}\)), các đường cao MA, NB cắt nhau tại I. Tia EI cắt MN tại H
a) c/m tam giác AMN = tam giác BNM
b) c/m EH là đường trung tuyến của tam giác EMN
c) Tính độ dài đoạn thẳng MA biết AE=3cm, AN=2cm
d) c/m I cách đều ba cạnh của tam giác ABH


a, Xét \(\Delta AMN\) và \(\Delta BMN\) có:
MN chung
góc ANM = góc BMN ( \(\Delta EMN\)cân)
góc MAN = góc NBM = 1v
b, Vì \(MA\perp EN\\ NB\perp EM\)
Mà \(MA\cap NB=\left\{I\right\}\)
Nên I là trực tâm của \(\Delta EMN\)
=> EH \(\perp MN\)
Do đó EH là đường trung tuyến của \(\Delta EMN\) ( T/c 3 đường cao của tam giác cân)
c, Ta có EN = EA+AN= 3 + 2 = 5(cm)
Mà \(\Delta EMN\)cân
=> EM = EN = 5cm
Áp dụng định lý Pytago, ta có:
\(ME^2=MA^2+AE^2\)
\(5^2=MA^2+2^2\)
\(MA^2=25-4\\ MA^2=21\)
MA = \(\sqrt{21}\)